Під структурно-складною системою з погляду аналізу надійності розумітимемо систему, що складається з довільної кількості довільно з'єднаних резервованих ланок (паралельно-послідовних, місткових). У попередніх лекціях було розглянуто два методи дослідження надійності структурно-складних систем: метод аналізу складних послідовно-паралельних структур, метод розкладання щодо особливого елемента. При великій кількості елементів та міжелементних зв'язків проведення розрахунків надійності цими методами є вкрай складним завданням. Автоматизація розрахунків дає змогу вирішити проблему аналізу надійності структурно-складних систем. Для здійснення автоматизації необхідно мати загальний формальний опис "надійної поведінки" аналізованої системи. Як такий опис було обрано алгебру логіки (див. додаток). Метод аналізу надійності складних систем, у якому їх структура описується засобами математичного апарату бінарної алгебри логіки, а кількісна оцінка надійності виробляється з допомогою теорії ймовірностей, отримав назву логіко-імовірнісного методу.
Застосування логіко-імовірнісних методів для визначення значень імовірнісних показників надійності в момент часу t для системи, що складається з елементів n, здійснюється в кілька етапів:
· Конструювання логічної функції працездатності системи
· Перетворення логічної функції до форми переходу до заміщення
· Отримання розрахункової ймовірнісної формули
1. Конструювання логічної функції працездатності (непрацездатності) системи
Робиться припущення про те, що як сама система, так і складові її елементи можуть бути лише у двох станах – працездатності та відмови, причому відмови елементів передбачаються незалежними. Тоді, з умов працездатності (непрацездатності) системи, можна сконструювати логічну функцію її працездатності S( x) (непрацездатності)
(1)
Аргументом функції S є вектор-рядок xлогічних змінних ,, таких що
(2)
Наприклад, якщо за вихідний опис системи прийняти вже вивчені нами блок-схеми надійності, то для системи, що складається з двох послідовно з'єднаних у значенні надійності елементів (відмова кожного є відмовою системи в цілому) (рис.1.а), , а . Функція працездатності дубльованої системи, у якій поодинокі відмови елементів не призводять до її відмови (рис.1.б), дорівнює , непрацездатності - . Для місткової структури (рис.1.в) . Ці функції побудовані досить формально - вони відображають наявність хоча б одного зв'язку (шляху) між входом і виходом схеми надійності системи. Шлях працездатний, якщо працездатні всі елементи, що до нього входять. Тому кожному шляху відповідає елементарна кон'юнкція змінних, що відповідають елементам, що входять у шлях, а S(X) – є диз'юнкція всіх елементарних кон'юнкцій, відповідних можливим шляхам від входу до виходу. Для систем невеликої розмірності запис подібних логічних виразів не становить труднощів, для складних систем, що складаються з великої кількості компонентів, потрібні спеціальні алгоритми проходу схеми та формування шляхів.
ЛОГІКО-ВЕРІЙНІ МЕТОДИ АНАЛІЗУ НАДІЙНОСТІ
Будь-який метод аналізу надійності вимагає опису умов працездатності системи. Такі умови можуть бути сформульовані на підставі:
структурної схеми функціонування системи (схеми розрахунку надійності);
Словесного опису функціонування системи;
Граф-схеми;
Функції логіки алгебри.
Логіко-імовірнісний метод аналізу надійності дозволяє формалізувати визначення та зміст сприятливих гіпотез. Сутність цього методу полягає в наступному.
· Стан кожного елемента кодується нулем та одиницею:
У функціях алгебри логіки стану елементів подаються у такому вигляді:
Х i- справний стан елемента, що відповідає коду 1;
Відмовний стан елемента, що відповідає коду 0.
Записується за допомогою функцій алгебри логіки умова працездатності системи через працездатність (стан) її елементів. Отримана функція працездатності системи є двійковою функцією двійкових аргументів.
Отримана ФАЛ перетворюється в такий спосіб, щоб у ній містилися члени, відповідні сприятливим гіпотезам справної роботи системи.
У ФАЛ замість двійкових змінних х iі підставляються ймовірності відповідно до безвідмовної роботи р iта ймовірності відмови q i.Знаки кон'юнкції та диз'юнкції замінюються алгебраїчним множенням та додаванням.
Отримане вираз і є ймовірність безвідмовної роботи системи P c (t).
Розглянемо логіко-імовірнісний метод на прикладах.
ПРИКЛАД 5.10.Структурна схема системи є основне (послідовне) з'єднання елементів (рис. 5.14).
На структурній схемі х i , i = 1, 2,..., п- стан i-го елемента системи, що кодується 0, якщо елемент знаходиться у відмовному стані, та 1, якщо він справний. В даному випадку система справна, якщо справні її елементи. Тоді ФАЛ є кон'юнкцією логічних змінних, тобто. у = x 1, x 2, ....., х п,являє собою досконалу диз'юнктивно нормальну форму системи.
Підставляючи замість логічних змінних ймовірності справних станів елементів і, замінюючи кон'юнкцію на множення алгебри, отримаємо:
ПРИКЛАД 5.11.Структурна схема системи є дубльованою системою з нерівнонадійними, постійно включеними підсистемами (рис. 5.15).
На рис. 5.15 х 1і х 2- Станки елементів системи. Складемо таблицю істинності двох двійкових змінних (табл. 5.2).
У таблиці 0 - стан стану елемента, 1 - справний стан елемента. В даному випадку система справна, якщо справні обидва елементи (1,1) або один з них ((0,1) або (1,0)). Тоді працездатний стан системи описується наступною функцією алгебри логіки:
Ця функція є досконалою диз'юнктивною нормальною формою. Замінюючи операції диз'юнкції та кон'юнкції на алгебраїчні операції множення та додавання, а логічні змінні - на відповідні ймовірності стану елементів, отримаємо ймовірність безвідмовної роботи системи:
ПРИКЛАД 5.12.Структурна схема системи має вигляд, показаний на рис. 5.16.
Складемо таблицю істинності (табл. 53).
У цьому прикладі система справна, якщо справні всі її елементи або справним є елемент x iта один з елементів дубльованої пари (х 2, х 3). На підставі таблиці істинності СДНФ матиме вигляд:
Підставляючи замість двійкових змінних відповідні ймовірності, а замість кон'юнкцій та диз'юнкцій – алгебраїчне множення та додавання, отримаємо ймовірність безвідмовної роботи системи:
Функцію алгебри логіки можна у мінімальній формі, якщо скористатися такими перетвореннями:
Операції поглинання та склеювання в алгебрі не застосовні. У зв'язку з цим не можна отриману ФАЛ мінімізувати, а потім замість логічних змінних підставляти значення ймовірностей. Імовірність станів елементів слід підставляти в СДНФ, а спрощувати за правилами алгебри.
Недоліком описаного методу є необхідність упорядкування таблиці істинності, що вимагає перебору всіх працездатних станів системи.
5.3.2. Метод найкоротших шляхів та мінімальних перерізів
Цей метод було розглянуто раніше у розд. 5.2.3.Викладемо його з позиції алгебри логіки.
Функцію працездатності можна описати за допомогою найкоротших шляхів пішого функціонування системи та мінімальних перерізів її відмови.
Найкоротшим шляхом називається мінімальна кон'юнкція працездатних: стоянь елементів, що утворюють працездатну систему.
Мінімальним перетином називається мінімальна кон'юнкція непрацездатних станів елементів, що утворюють непрацездатний стан системи.
ПРИКЛАД 5.13.Необхідно утворити функцію працездатності системи, структурна схема якої наведена на рис. 5.17, використовуючи метод найкоротших шляхів та мінімальних перерізів.
Рішення.В даному випадку найкоротшими шляхами, що утворюють працездатну систему, будуть: х 1 х 2, х 3 х 4, х 1 х 5 х 4, х 3 х 5 х 2 .Тоді функція працездатності запишеться у вигляді наступної функції логіки алгебри:
Відповідно до цієї ФАЛ структурна схема системи рис. 5.17 може бути представлена структурною схемою рис. 5.18.
Мінімальними перерізами, що утворюють непрацездатну систему, будуть: х 1 х 3, х 2 х 4, х 1 х 5 х 4, х 3 х 5 х 2 .Тоді функція непрацездатності запишеться у вигляді наступної функції логіки алгебри:
Відповідно до цієї ФАЛ структурна схема системи буде представлена у вигляді, показаному на рис. 5.19.
Слід пам'ятати, що структурні схеми рис. 5.18 та рис. 5.19 не є схемами розрахунку надійності, а вирази для ФАЛ працездатного та непрацездатного станів не є виразами для визначення ймовірності безвідмовної роботи та ймовірності відмови:
Основні переваги ФАЛ в тому, що вони дозволяють отримати формально, не складаючи таблиці істинності, СДНФ та СКНФ (досконала кон'юнктивна нормальна форма), які дають можливість отримати ймовірність безвідмовної роботи (ймовірність відмови) системи шляхом підстановки у ФАЛ замість логічних змінних відповідних значень ймовірностей роботи, замінивши операції кон'юнкції та диз'юнкції на алгебраїчні операції множення та додавання.
Для отримання СДНФ необхідно кожен диз'юнктивний член ФАЛ помножити на де х i- відсутній аргумент, і розкрити дужки. Відповіддю буде СДНФ. Розглянемо цей метод з прикладу.
ПРИКЛАД 5.14.Необхідно визначити можливість безвідмовної роботи системи, структурна схема якої наведена на рис. 5.17. Імовірності безвідмовної роботи елементів дорівнюють р 1, р 2, р 3, р 4, р 5 .
Рішення.Скористаємося методом найкоротших шляхів. Функція алгебри логіки, отримана методом найкоротших шляхів, має вигляд:
Отримаємо СДНФ системи. Для цього помножимо диз'юнктивні члени на:
Розкриваючи дужки та виконуючи перетворення за правилами алгебри логіки, отримаємо СДНФ:
Підставляючи в СДНФ замість х 1, х 2, х 3 , х 4, х 5ймовірності безвідмовної роботи р 1, р 2, р 3, р 4, р 5та використовуючи співвідношення q i = 1–р i, Отримаємо наступне вираз для ймовірності безвідмовної роботи системи.
З наведеного прикладу видно, що спосіб найкоротших шляхів звільнив нас від визначення сприятливих гіпотез. Той самий результат можна отримати, якщо скористатися методом мінімальних перерізів.
5.3.3. Алгоритм розрізання
Алгоритм розрізання дозволяє отримати ФАЛ, підставляючи яку замість логічних змінних ймовірності безвідмовної роботи (ймовірності відмови) елементів можна знайти ймовірність безвідмовної роботи системи. Одержання цієї мети СДНФ не требуется.
Алгоритм розрізання заснований на наступній теоремі алгебри логіки: функція алгебри логіки у (х ь х 2, ..., х п)може бути представлена в наступній формі:
Покажемо застосування цієї теореми на трьох прикладах:
Застосовуючи другий розподільчий закон алгебри логіки, отримаємо:
ПРИКЛАД 5.15.Визначити можливість безвідмовної роботи системи, структурна схема якої представлена на рис. 5.16, скориставшись алгоритмом розрізання.
Рішення.Використовуючи метод найкоротших шляхів, отримаємо наступну ФАЛ:
Застосуємо алгоритм розрізання:
Підставляючи тепер замість логічних змінних ймовірності та замінюючи операції кон'юнкції та диз'юнкції на алгебраїчне множення та додавання, отримаємо:
ПРИКЛАД 5.16.Визначити можливість безвідмовної роботи системи, структурна схема якої наведена на рис. 5.17. Скористайтеся алгоритмом розрізання.
Рішення.Функція алгебри логіки, отримана методом мінімальних перерізів, має вигляд:
Реалізуємо алгоритм розрізань щодо х 5:
Спростимо отриманий вираз, користуючись правилами логіки алгебри. Вираз у перших дужках спростимо, використовуючи правило виносу за дужки:
Тоді ФАЛ матиме вигляд:
Цьому виразу відповідає структурна схема рис. 5.20.
Отримана схема також є схемою розрахунку надійності, якщо логічні змінні замінити ймовірностями безвідмовної роботи. р 1 , р 2 , р 3 , р 4 , р 5а змінну – ймовірністю відмови q 5 .З рис. 5.20 видно, що структурна схема системи зведена до послідовно-паралельної схеми. Імовірність безвідмовної роботи обчислюється за такою формулою:
Формула пояснення не потребує, вона записана безпосередньо за структурною схемою.
5.3.4. Алгоритм ортогоналізації
Алгоритм ортогоналізації, як і алгоритм розрізання, дозволяє формальними процедурами утворити функцію алгебри логіки, підставляючи яку замість логічних змінних ймовірності, а замість диз'юнкцій і кон'юнкції - алгебраїчне додавання і множення, отримати ймовірність безвідмовної роботи системи. Алгоритм заснований на перетворенні функцій алгебри логіки в ортогональну диз'юнктивну нормальну форму (ОДНФ), яка суттєво коротша за СДНФ. Перш ніж викладати методику, сформулюємо ряд визначень та наведемо приклади.
Дві кон'юнкціїназиваються ортогональними,якщо їх твір тотожний нуль. Диз'юнктивна нормальна форманазивається ортогональна,якщо всі її члени попарно ортогональні. СДНФ є ортогональною, але найдовшою з усіх ортогональних функцій.
Ортогональну ДНФ можна отримати за допомогою таких формул:
Ці формули легко довести, якщо скористатися другим розподільчим законом алгебри логіки та теоремою де-Моргана. Алгоритмом отримання ортогональної диз'юнктивної нормальної форми є наступна процедура перетворення функції у (х 1, х 2, ..., х п)в ОДНФ:
Функція у (х 1, х 2, ..., х п)перетворюється на ДНФ за допомогою методу найкоротших шляхів або мінімальних перерізів;
Знаходиться ортогональна диз'юнктивно-нормальна форма за допомогою формул (5.10) та (5.11);
Мінімізується функція шляхом прирівнювання до нуля ортогональних членів ОДНФ;
Логічні змінні замінюються ймовірностями безвідмовної роботи (імовірностями відмов) елементів системи;
Остаточне рішення виходить після спрощення виразу, отриманого на попередньому етапі.
Розглянемо методику з прикладу.
ПРИКЛАД 5.17.Визначити можливість безвідмовної роботи системи, структурна схема якої наведена на рис. 5.17. Застосувати метод ортогоналізації.
Рішення.У разі функціонування системи описується наступною функцією алгебри логіки (метод мінімальних перерізів):
Позначимо До 1= х 1 х 2 , До 2= х 3 х 4, До 3= х 1 х 5 х 4, До 4 = х 3 х 5 х 2. Тоді ОДНФ запишеться у такому вигляді:
Значення , i= 1,2,3, на підставі формули (5.10) матимуть вигляд:
Підставляючи ці вирази (5.12), отримаємо:
Замінюючи в цьому виразі логічні змінні відповідними ймовірностями і виконуючи операції алгебри складання та множення, отримаємо ймовірність безвідмовної роботи системи:
Відповідь збігається з одержаним у прикладі 5.14.
З прикладу видно, що алгоритм ортогоналізації продуктивніший, ніж способи, розглянуті раніше. Докладніше логіко-імовірнісні методи аналізу надійності викладені в . Логіко-імовірнісний метод, як і будь-який інший, має свої переваги та недоліки. Про його переваги було сказано раніше. Вкажемо його недоліки.
Вихідними даними в логіко-імовірнісному методі є ймовірність безвідмовної роботи елементів структурної схеми системи. Однак у багатьох випадках ці дані неможливо отримати. І не тому, що надійність елементів невідома, а тому, що час функціонування елемента є випадковою величиною. Це має місце у разі резервування заміщенням, наявності післядії відмов, неодночасності роботи елементів, наявності відновлення з різною дисципліною обслуговування та в багатьох інших випадках.
Наведемо приклади, що ілюструють ці недоліки. Структурна схема системи має вигляд, показаний на рис. 5.21, де прийняті такі позначення: x i- логічні змінні, що мають значення 0 і 1, відповідні відмові та справній роботі елемента, x i = 1, 2, 3.
У даному випадку логічна змінна дс 3 є 0 до моменту часу відмовлення основного елемента і 1 протягом часу (t-τ),де t- брешемо, протягом якого визначається ймовірність безвідмовної роботи системи. Час τ є величиною випадковою, тому значення р(τ)невідомо. У разі скласти ФАЛ і більше СДНФ неможливо. Жоден із розглянутих нами логіко-імовірнісних методів не дозволяє знайти ймовірність безвідмовної роботи системи.
Ось ще один типовий приклад. Енергетична система складається з регулятора напруги. Rн і двох паралельно працюючих генераторів Г1 і Г2. Структурна схема системи показано на рис. 5.22.
При відмові одного з генераторів, що залишився справним, працює один загальне навантаження. Його інтенсивність відмов зростає. Якщо до моменту τ відмови одного з генераторів інтенсивність його відмови дорівнювала λ , то після відмови λ 1 > λ 2. Оскільки час τ є величиною випадковою, то Р(τ)невідомо. Тут, як і у разі резервування заміщенням, логіко-ймовірні методи безсилі. Таким чином, зазначені недоліки логіко-імовірнісних методів знижують їхнє практичне застосування при розрахунку надійності складних систем.
5.4. Топологічні методи аналізу надійності
Топологічними називатимемо методи, які дозволяють визначити показники надійності або за графом станів, або за структурною схемою системи, не складаючи і не вирішуючи рівнянь. Топологічним методам присвячено ряд робіт, в яких описані різні способи їхньої практичної реалізації. У цьому розділі викладаються методи, що дозволяють визначити показники надійності за станом.
Топологічні методи дають можливість обчислювати такі показники надійності:
- Р(t)- можливість безвідмовної роботи протягом, часу t;
- T 1, - Середній час безвідмовної роботи;
- К г (t)- функцію готовності (імовірність того, що система справна у будь-який довільний момент часу t);
- До г= - Коефіцієнт готовності;
T- Напрацювання на відмову відновлюваної системи.
Топологічні методи мають такі особливості:
Простота обчислювальних алгоритмів;
Висока наочність процедур визначення кількісних характеристик надійності;
Можливість наближених оцінок;
Відсутність обмежень на вигляд структурної схеми (системи, що відновлюються та не відновлюються, нерезервовані та резервовані з будь-яким видом резервування та будь-якою кратністю).
У цьому розділі розглядатимуться обмеження топологічних методів:
Інтенсивності відмов та відновлення елементів складної системи є величинами постійним»;
Тимчасові показники надійності, такі як можливість безвідмовної роботи та функція готовності, визначаються в перетвореннях Лапласа;
Проблеми, часом непереборні, під час аналізу надійності складних систем, описуваних многосвязным графом станів.
Ідея топологічних методів полягає у наступному.
Граф станів є одним із способів опису функціонування системи. Він визначає вид диференціальних рівнянь та їх кількість. Інтенсивності переходів, що характеризують надійність елементів та його відновлюваність, визначають коефіцієнти диференціальних рівнянь. Початкові умови обираються кодуванням вузлів графа.
У графі станів міститься вся інформація про надійність системи. І це є підставою вважати, що показники надійності може бути обчислені безпосередньо за графом станів.
5.4.1. Визначення ймовірностей станів системи
Імовірність застати систему, що відновлюється, в стані iу фіксований момент часу tу перетворенні Лапласа може бути записана в наступному вигляді:
де Δ(s)- головний визначник системи диференціальних рівнянь, записаної у перетворення Лапласа; Δ i (s)- Приватний визначник системи.
З виразу (5.13) видно, що Pi (s)буде визначено, якщо з графа станів буде знайдено ступеня типполіномів чисельника та знаменника, а також коефіцієнти B ij (j = 0,1,2,..., m) та А і(i = 0,1, 2,..., n-1).
Спочатку розглянемо методику визначення Pi (s)графа станів лише таких систем, у графі станів яких відсутні переходи через стани. До них відносяться всі надлишкові системи, резервовані системи при загальному резервуванні з цілою і дробовою кратністю, резервовані системи будь-якої структури з обслуговуванням пристроїв, що відмовили в послідовності, зворотній їх надходженню в ремонт. До зазначеного класу систем належать деякі резервовані системи з рівнонадійними пристроями при різній дисципліні їх обслуговування.
Функціонування системи описується диференціальними рівняннями, число яких дорівнює числу вузлів графа. Це означає, що головний визначник системи Δ(s)у загальному випадку буде поліномом n-й ступеня, де n- Число вузлів графа стані. Легко показати, що поліном знаменника немає вільного члена. Справді, т.к. то знаменник функції Pi (s)повинен містити sяк співмножник, інакше фінальна ймовірність Pi (∞)дорівнюватиме нулю. Винятком є випадки, коли кількість ремонтів обмежена.
Ступінь полінома чисельникаΔ i знаходиться з виразу:
m i = n - 1 – l i,
де n- Число вузлів графа станів; l i- Число переходів з початкового стану системи, визначеного початковими умовами її функціонування, в стан iнайкоротшим шляхом.
Якщо початковим станом системи є стан, коли всі пристрої справні, то l i- Номер рівня стану i, тобто. l iдорівнює мінімальному числу пристроїв системи, що відмовили, в стані i. Таким чином, ступінь полінома чисельника ймовірності Р i (s)перебування системи в i-м стані залежить від номера стану iта від початкових умов. Оскільки кількість переходів l iможе бути 0,1,2,..., n-1, то ступінь поліномаΔ i (s) на підставі (5.14) також може приймати значення m i = 0,1,2,..., n-1.
ЛВМ виникла в результаті досліджень проблем безпеки складних систем. З його допомогою можна оцінити можливість відмови складної системи.
ЛВМ відноситься до аксіоматичних методів прийняття рішень в умовах стохастичної невизначеності. Він дозволяє знизити цю невизначеність своїм доказовим підходом та результатами експериментів – імовірнісними характеристиками альтернатив.
У посібнику ЛВМ розглянуто з прикладу вирішення завдання вибору найбільш надійної інформаційної системи.
Нехай багато альтернатив – це безліч показників ризиків інформаційних систем (ІВ). Потрібно знайти таку ІВ, ризик якої мінімальний.
Під ризиком системирозглядається сума ризиків ресурсів, з яких вона складається:
де R i- Ризик i-го ресурсу, n– кількість ресурсів. З кожним ресурсом пов'язано безліч небезпечних станів (ОС), реалізація яких призводить до відмови цього ресурсу.
Як приклади ресурсів ІС можуть виступати інформаційні ресурси, послуги, фізичні чи апаратні ресурси, програмне забезпечення. Одним із прикладів інформаційного ресурсу може бути база даних ІС.
Під ризиком i-го ресурсурозуміється сума ризиків, пов'язаних із реалізацією небезпечних станів даного ресурсу:
де r i j– ризик реалізації j-го небезпечного стану i-го ресурсу, ; M i– кількість небезпечних станів i-го ресурсу
Прикладами ОС для ресурсу «БД» є порушення конфіденційності інформації, повна чи часткова втрата інформації через вихід носія інформації, порушення доступу.
Під ризиком реалізації j-го небезпечного стану i-го ресурсурозуміється твір ймовірності P ijта вартості втрат C ijвід реалізації цього небезпечного стану ресурсу:
.
Таким чином, завдання оцінки ризику системи можна розбити на такі етапи:
1. опис структури ресурсів системи;
2. опис безлічі небезпечних станів ресурсів системи;
3. оцінка ймовірностей P ijреалізації небезпечних станів, у тому числі виявлення міри впливу загроз на реалізацію небезпечних станів;
4. оцінка вартості втрат C ijвід небезпечних станів.
Основні положення логіко-імовірнісного методу
Логіко-імовірнісний метод аналізу безпеки складних технічних систем був запропонований у 70-х роках 20 століття
І. А. Рябініним. Основна ідея цього методу полягає у поєднанні логічного та ймовірнісного підходів при оцінці показників надійності складних технічних, економічних, соціальних систем та інших систем.
У ЛВМ як базові використовуються поняття небезпечного стану системи і небезпеки - Можливості системи переходити в небезпечний стан. Опис небезпечного стану системи починається зі складання сценарію небезпечного стану (ОС), який будується з використанням операцій диз'юнкція та кон'юнкція над ініціюючими умовами і подіями .
Як ініціюють умов і подій виступають відмови одного чи кількох елементів системи. Кожному елементу системи ставиться у відповідність логічна змінна x k() з двома можливими станами (наприклад, працездатності/відмови, готовності/неготовності тощо) з заданими імовірнісними параметрами цих станів p kі q k =1-p k.
Сценарій є основою для складання логічної функції, або алгебри логіки (ФАЛ), що описує небезпечний стан системи.
Наступним кроком є перетворення алгебри функції логіки до ймовірнісної функції, яка надалі використовується для отримання кількісної оцінки ймовірності реалізації небезпечного стану.
Таким чином, з одного боку, метод надає механізм для формалізації множини небезпечних станів системи, а з іншого боку – теоретично обґрунтований підхід до кількісної оцінки ризику системи.
Для системи, що з різних ресурсів, ЛВМ використовується з метою отримання кількісних оцінок ймовірностей реалізації небезпечних станів кожного виду ресурсів. Своєю чергою, кожен ресурс у ЛВМ також розглядається як окрема система.
Постановка задачі оцінки ймовірностей реалізації небезпечних станів ресурсу
Дано:
1. Ресурс із номером i, для якого виділено небезпечні стани S ij, , де m- Число можливих станів.
2. Структура ОС та ймовірності ініціюючих подій (загроз) x k, .
Потрібно знайти:
Ймовірності P ijреалізації небезпечних станів S ij, .
Алгоритм рішення
Крок 1. Складання сценарію небезпечного стану S ij.
Крок 2. Побудова алгебри функції логіки (ФАЛ) 
з використанням операцій кон'юнкція та диз'юнкція на основі сценарію небезпечного стану S ij.
Крок 3. Побудова імовірнісної функції (ВФ) 
з урахуванням функції алгебри логіки.
Крок 4. Розрахунок ймовірності P ijреалізації небезпечного стану за допомогою імовірнісної функції.
Теоретичні основи ЛОМ
В даний час математична логіка та теорія ймовірностей поєднуються на основі логіко-ймовірнісного обчислення. У цьому передбачається, що теорія ймовірностей дозволяє кількісно оцінювати надійність чи безпеку систем, структура яких описується засобами математичної логіки.
Основною проблемою в практичному застосуванні ЛОМ є перетворення довільних ФАЛ до форм переходу до повного заміщення (ФППЗ). Для того щоб зробити це перетворення стандартним та математично суворим, необхідно звернутися до спеціального теоретичного апарату, основні поняття та теореми якого будуть наведені нижче.
Вважатимемо, що кожному елементу системи ставиться у відповідність логічна змінна x k ,() з двома можливими станами (працездатності/відмови, готовності/не готовності тощо) з заданими ймовірнісними параметрами цих станів p kі q k =1-p k :
Крім того, робиться припущення, що всі події x kє незалежними в сукупності і що на інтервалі часу роботи системи, що розглядається, вихідні параметри законів розподілів елементів не змінюються.
Вираз виду 
називається елементарною кон'юнкцією
Kрангу r. Вираз виду , де елементарні кон'юнкції різних рангів, називається диз'юнктивною нормальною формою
(ДНФ). Якщо функція записана в ДНФ, причому ранг кожної елементарної кон'юнкції дорівнює n, то така ДНФ називається досконалою диз'юнктивною нормальною формою
(СДНФ).
Вираз виду 
називається елементарною диз'юнкцією
рангу r.
Дві елементарні кон'юнкції називаються ортогональними , якщо їх добуток дорівнює нулю (приклад: і).
ДНФ називається ортогональна диз'юнктивна нормальна форма (ОДНФ), якщо всі її члени попарно ортогональні.
Безповторний ДНФ(БДНФ) називається така ДНФ, у якій кожна логічна змінна зустрічається рівно один раз.
Правила де Морганадозволяють логічне множення висловити через заперечення логічної суми інверсій висловлювань, а логічну суму – через заперечення логічного твору інверсного висловлювання. Надалі вони будуть використовуватися для приведення ФАЛ до спеціального виду:
і 
Ймовірнісною функцією(ВФ) називатимемо ймовірність істинності ФАЛ:
P(f(x 1 , x 2 , …, x h)=1 )
Функції алгебри логіки, що допускають безпосередній перехід до ймовірнісної функції заміною логічних змінних ймовірностей, а логічних операцій відповідними арифметичними операціями, назвемо формами переходу до заміщення (ФПЗ).
Формами початку повного заміщення(ФППЗ) називаються ФПЗ, у яких проводиться заміщення одночасно всіх логічних змінних.
Булевою різницеюфункції 
за аргументом x kназивається
де символом « » позначено логічна операція «сума за модулем два».
Функція 
називається монотонної
, якщо для будь-яких наборів ( a 1 , …, a h) та ( b 1 , …, b h), таких, що , ( k=1,2,…,h) має місце співвідношення f(a 1 , …, a h) f(b 1 , …, b h). Далі розглянемо низку основних теорем.
Теорема 1.Приватна похідна від імовірності істинності монотонної ФАЛ за імовірністю істинності аргументу x kчисельно дорівнює ймовірності істинності булевої різниці цієї функції за аргументом x k:
Теорема 2.Імовірність істинності довільної ФАЛ, представленої в ОДНФ, дорівнює сумі ймовірностей істинності всіх ортогональних членів цієї ФАЛ:
,
де O u- Не тільки елементарні кон'юнкції ОДНФ, але і будь-які ФАЛ, попарно ортогональні.
Теорема 3.Диз'юнкція ортогональних безповторних форм у базисі кон'юнкція-заперечення є формою початку повного заміщення.
Нині відомо кілька ФППЗ – це досконала диз'юнктивна нормальна форма (СДНФ), ортогональна диз'юнктивна нормальна форма (ОДНФ) та безповторні ФАЛ (БФАЛ) у базисі «кон'юнкція-заперечення».
Якщо ФАЛ представлена у ФППЗ, то перехід до ймовірнісної функції здійснюється за такими правилами:
1. Кожна логічна змінна у ФППЗ замінюється ймовірністю її рівності одиниці:
, ;
2. Заперечення функції замінюється різницею між одиницею та ймовірністю рівності цієї функції одиниці;
3. Операції логічного множення та додавання замінюються операціями арифметичного множення та додавання.
Складання сценарію небезпечного стану
Складання сценарію небезпечного стану ІВ можна представити у вигляді наступної послідовності кроків:
1. виділення кінцевого події – небезпечного стану (відмови),
2. виділення проміжних подій, що призводять до реалізації небезпечного стану та одержуються як комбінація двох або більше ініціюючих подій,
3. виділення ініціюючих подій-загроз.
Для подання небезпечного стану використовується дерево подій або відмов.
На рис. 5.2 наведено приклад сценарію небезпечного стану у вигляді дерева подій.
Мал. 5.2. Приклад дерева подій для опису небезпечного стану системи
Побудова алгебри функції логіки
За допомогою дерева подій складається функція логіки алгебри, що описує умови переходу системи в небезпечний стан.
Для опису умов переходу системи до небезпечного стану використовується поняття « найкоротший шлях небезпечного функціонування »(КПОФ), під яким розуміється кон'юнкція мінімального набору елементів системи, що забезпечують разом перехід системи у небезпечний стан:
,
де K wl– безліч номерів змінних, які відповідають цьому шляху.
Умова переходу системи у небезпечний станможна подати у вигляді диз'юнкції всіх наявних КПОФ:
.
приклад.Нехай дерево подій має вигляд, представлений на рис. 5.2.
Тоді КПОФ є: , , , .
Умова переходу системи в небезпечний стан має вигляд:
Побудова імовірнісної функції
На попередньому етапі було отримано ФАЛ 
, Яка описує небезпечний стан системи як диз'юнкцію всіх КПОФ Наступним кроком є перетворення ФАЛ до ФППЗ – СДНФ, ОДНФ чи безповторної ФАЛ у базисі кон'юнкція-заперечення (БФАЛ).
Побудова імовірнісної функції на основі ФППЗ здійснюється згідно з правилами, описаними вище. Результатом цього етапу є імовірнісна функція
Розрахунок оцінки ймовірності реалізації небезпечного стану
Підставляючи значення 
у ВФ, отриману на попередньому етапі, отримуємо оцінку ймовірності реалізації небезпечного стану P ij.
приклад
Розглянемо приклад застосування ЛОМ для оцінки ризику реалізації небезпечного стану «Порушення конфіденційності бази даних ІС (БД ІВ)».
Крок 1.Упорядкування сценарію небезпечного стану ресурсу (рис. 5.3).
Мал. 5.3. Сценарій ОС «Порушення конфіденційності БД ІВ»
Крок 2Побудова функції алгебри логіки. Згідно з описаним сценарієм, логічна функція набуває вигляду:
F=X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 12 X 13 X 14 X 15 X 12 X 13 X 14 X 15
електропостачання за допомогою дерева відмов
Логіко-імовірнісний метод з використанням дерева відмов є дедуктивним (від загального до приватного) і застосовується в тих випадках, коли кількість різних відмов системи відносно невелика. Застосування дерева відмов для опису причин відмови системи полегшує перехід від загального визначення відмови до приватним визначенням відмов та режимів роботи її елементів, зрозумілим фахівцям-розробникам як самої системи, так і елементів. Перехід від дерева відмов до логічної функції відмови відкриває можливості для аналізу причин відмови системи на формальній основі. Логічна функція відмови дозволяє отримати формули для аналітичного розрахунку частоти та ймовірності відмов системи за відомою частотою та ймовірностями відмов елементів. Використання аналітичних виразів при розрахунку показників надійності дає підстави для застосування формул теорії точності з метою оцінки середньоквадратичної похибки результатів.
Відмова функціонування об'єкта як складна подія є сумою події відмови працездатності та події 
, що полягає у появі критичних зовнішніх впливів Умова відмови функціонування системи формулюється фахівцями в галузі конкретних систем на основі технічного проекту системи та аналізу її функціонування у разі виникнення подій за допомогою висловлювань.
Висловлювання може бути кінцевими, проміжними, первинними, простими, складними. Просте висловлювання відноситься до події чи стану, які самі не розглядаються ні як логічна сума «АБО», ні як логічний твір «І» інших подій чи станів. Складне висловлювання, що є диз'юнкцією кількох висловлювань (простих чи складних), позначається оператором «АБО», що пов'язує висловлювання нижчого рівня з висловлюваннями вищого рівня (рис.3.15,а). Складне висловлювання, що є кон'юнкцією кількох висловлювань (простих чи складних), позначається оператором «І», що пов'язує висловлювання нижчого рівня з висловлюваннями вищого рівня (рис.3.15,б).
Рис.3.15.Елементи подання логічних схем
Висловлювання зручно кодувати так, щоб за кодом можна було судити про те, просте воно або складне, на якому рівні від кінцевого розташоване і що є (подія, стан, відмова спрацьовування, тип елемента).
Теоретично графів деревом називається зв'язковий граф, який містить замкнутих контурів. Деревом відмов називають логічне дерево (рис. 3.16), в якому дуги становлять події відмови на рівні системи, підсистем або елементів, а вершини – логічні операції, що пов'язують вихідні та результуючі події відмов.
Мал. 3.16.Приклад побудови дерева відмов
Побудова дерева відмов починається з формулювання кінцевого висловлювання про відмову системи. Для характеристики безвідмовності системи кінцеве висловлювання відносять до події, що призводить до порушення функціонування в інтервалі часу, що розглядається, за заданих умов. Те саме для характеристики готовності.
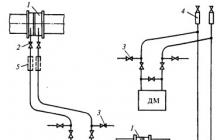
Приклад 8. Побудуємо дерево відмов для схеми мережі, наведеної на рис.3.17.
Рис.3.17.Схема мережі
Підстанції Уі Зхарчуються від підстанції А. Кінцевою подією дерева відмов є відмова системи загалом. Ця відмова визначається як подія, яка полягає в тому, що
1) чи підстанція У, або підстанція Зповністю втрачають харчування;
2) потужність для живлення сумарного навантаження підстанцій Уі Здоводиться передавати по одній лінії.
Виходячи з визначення кінцевої події та принципової схеми системи, будуємо дерево відмов (вниз від кінцевої події) (рис. 3.18). Мета аналізу дерева відмов полягає в тому, щоб визначити можливість кінцевої події. Оскільки кінцева подія є відмова системи, аналіз дає можливість Р(F).
Метод аналізу заснований на знаходженні та розрахунку множин мінімальних перерізів. Перетиномназивають таку безліч елементів, сумарна відмова яких призводить до відмови системи. Мінімальний переріз - така безліч елементів, з якого не можна видалити жодного елемента, інакше він перестає бути перетином.
Пересуваючись на один рівень нижче від вершинної (кінцевої) події, проходимо через вузол «АБО», який вказує на існування трьох перерізів: ( P}, {Q}, {R} (Р,Q, R- Події відмов). Кожен із цих перерізів може бути поділено далі на більшу кількість перерізів, але може з'ясуватися, що відмова перерізів обумовлюється кількома подіями, залежно від того, який тип логічного вузла зустрічається на шляху прямування.
Рис.3.18.Дерево відмов системи за схемою рис. 3.17:
-відмови підсистем, які можна аналізувати далі;
Наприклад, (Q) спочатку перетворюється на переріз (3, Т), потім Тподіляється на перерізи ( Х,У), в результаті замість одного перерізу (3, Т) з'являються два: (3, X}, {3,У}.
На кожному з наступних кроків виявляються множини перерізів:
Мінімальними перерізами є виділені перерізи (3,4,5), (2,3), (1,3), (1,2). Перетин (1,2,3) не мінімальний, оскільки (1,2) – теж перетин. На останньому етапі безлічі перерізів складаються виключно з елементів.
Завдання
Обчислити ймовірність безвідмовної роботи P cсистеми зі структурою та параметрами, заданими у п.6.4, логіко-імовірнісним методом. Порівняти отриманий результат із граничними оцінками, отриманими у п.6.
Елементи теорії
Нехай x=(x 1 ,..., x n) - n-мірний вектор, що характеризує стан системи, де х i- Бульова змінна: х i= 1 , якщо i-я підсистема працездатна, і, x i = 0 інакше.
Ввівши відповідний критерій відмови для системи, можна задати булеву функцію, що описує стан працездатності або відмови системи:
R (x) = 1, якщо система працездатна. R(x)=0якщо система відмовляє.
Якщо система перебуває у стані відмови. якщо система працездатна.
Тут R(х) - функція працездатності, - функція відмови у стані х.
Перейдемо до ймовірнісних функцій:
Тут Р- можливість безвідмовної роботи системи і Q- ймовірність відмови системи, визначені для випадку, коли х iвідповідає працездатному стану i-го елемента (підсистеми) Рі Qтут визначено для того ж моменту часу, що й р(х i) та q(х i) - ймовірності безвідмовної роботи та відмови елементів.
Структура системи називається монотонною, якщо для функції R(х) Виконуються такі умови:
а) R(1)= 1 де 1 =(1 ,...,1);
б) R(0) = 0, де 0 = (0, ..., 0);
в) R(х) ≥R(у), якщо х ≥у,
де умова (в) розуміється як сукупність пумов х i ≥у i.
Для оцінки надійності таких систем застосовуються метод мінімальних шляхів і мінімальних перерізів, логіко-всроятностнчй метод та інші.
До монотонних структур відносяться послідовно-паралельні та паралельно-послідовні структури, а також незведені до них , такі, наприклад, як "місткові".
Приклад рішення
Застосування логіко-імовірнісного методу, що дозволяє одержати точне значення ймовірності безвідмовної роботи, розглянемо на прикладі місткової структури, представленої на рис. 6.1.
функцію R (х)представимо у диз'юнктивній нормальній формі (ДНФ) безліччю мінімальних шляхів (див. п.6.2)
R(х) = x 1 х 4 V х 1 x 3 x 5 V х 2 х 5 V х 2 x 3 х 4
де х i -булева змінна, що визначає стан працездатності i-гоелемент. Матрична форма булевої функції R(х)представлена рис 7.1.
Для обчислення Р знеобхідно R(х)подати в ортогональній формі R орт, тобто. у вигляді безлічі інтервалів, що не перетинаються.
І відповідно до матриці рис. 7.1 маємо:
Для обчислення достатньо (7.1) х iзамінити на р i , на 1 -p i , кон'юнкцію - на твір та диз'юнкцію - у сумі. Зробивши це, отримаємо:
Нехай p i = p=0,8 тоді,
Порівняння із результатом, отриманим у п. 6.3. дає:
0,9069<0,9611<0,9692
бібліографічний список
1. Козлов Б.А., Ушаков І.А. Довідник з розрахунку надійності апаратури радіоелектроніки та автоматики. - М.: Рад.радіо, 1975. - 472 с.
2. Іуду К.А. Надійність, контроль та діагностика обчислювальних машин та систем. - М.: Вищ.шк., 1989. - 216 с.
3. Надійність технічних систем: Довідник/Ю.К. Бєляєв, В.А. Богатирьов та ін; За ред. І.А. Ушакова. - М.: Радіо та зв'язку, 1985. - 608 с.
4. Дружинін Г.В. Надійність автоматизованих виробничих систем. - 4-те вид. - М.: Енергоатом-видав, 1986. - 480 с.
5. Каган Б.М., Мкртумян І.Б. Основи експлуатації ЕОМ. - М.: Вища школа, 1988. - 432 с.
