ピラミッドは豊かな顔に基づいた豊かな顔です。 すべてのエッジは、1 つの頂点に集まるトリキュビチュールによって独自の形状を形成します。 ピラミッドには、3 ピース、4 点などがあります。 どのピラミッドが目の前にあるかを判断するには、そのスタンドにあるいくつかのキュータをつかむ必要があります。 「ピラミッドの高さ」の意味は、学校のカリキュラムの幾何学の課題でよく指定されます。 それを見つけるさまざまな方法を見てみましょう。
ピラミッドの一部
皮膚ピラミッドは次の要素で構成されています。
- ビッチエッジ、それらは三つに揺れ、頂上に集まります。
- 頂点はその頂点から下りた高さです。
- ピラミッドの頂点はサイドリブを接続する点ですが、ベースの平面上にはありません。
- 基礎は金持ちであり、その上に頂点はありません。
- ピラミッドの高さは、ピラミッドの上部を横切り、周囲に直線のカットを作成するカットです。
知られているピラミッドの高さを見つける方法

式 V = (S * h) / 3 (式中、V は体積、S はスタンドの面積、h はピラミッドの高さ) を通して、h = (3 * V) / S であることがわかります。資料を統合するには、すぐにzavdannyaをしましょう トリカットの底面はまだ 50 cm 2 であるため、その体積は 125 cm 3 になります。トリカット ピラミッドの高さは不明なので、これを知る必要があります。 ここではすべてが簡単です。データを数式に挿入します。 h = (3 * 125) / 50 = 7.5 cm としましょう。
対角線とその辺の長さを見てピラミッドの高さを知る方法
覚えているように、ピラミッドの高さにより、その底部には直線的なカットが作成されます。 これは、高さ、端、対角線の半分が同時に作成されることを意味し、したがってピタゴラスの定理が成り立ちます。 2 つの量がわかっている場合、3 番目の量を知ることは困難になります。 私たちは定理 a² = b² + c² を知っています。ここで、a は斜辺であり、この場合はピラミッドの端です。 b - 最初の脚または対角線の半分、h - 同様のもう一方の脚、またはピラミッドの高さ。 これは公式 c² = a² - b² です。
ここで問題は、正しいピラミッドでは、対角線は依然として 20 cm ですが、辺の長さは 30 cm であるため、高さを知る必要があります。 事実上: c² = 30² - 20² = 900-400 = 500。Star z = √ 500 = 22.4 に近い。
角錐台の高さの求め方
ボーンは豊かな低木で、根元と平行に走っています。 角錐台の高さは、その 2 つの部分を接続するカットです。 高さは次から求めることができます 正しいピラミッド, 両方の底辺の 2 つの対角線とピラミッドの端が表示されるので、 大きいスタンドの対角線は d1 に等しく、小さいスタンドの対角線は d2 で、エッジは l と同じです。 高さを求めるには、図を使用して、ベースの最上部 2 点からの高さを下げることができます。 直線3枚切りを2頭持っている我々バチモは、その脚の全容を知ることはできないだろう。 これについては、対角線を大きくすると、最小値がわかり、2 で割られます。したがって、一方の辺がわかります: a = (d1-d2) / 2。その後、ピタゴラスの定理によれば、もう一方の辺を知ることができなくなります。 、高さは n iramidi です。

それでは、実際に右からすべてを見てみましょう。 私たちの前には荒野があります。 角錐台は底面が正方形で、大きい底面の対角線が10cm、小さい底面の対角線が6cm、辺が4cmの高さを知る必要があります。 穂軸の場合、片方の脚は a = (10-6) / 2 = 2 cm であることがわかります。一方の脚は 2 cm 以上、斜辺は 4 cm です。もう一方の脚または高さはそれより大きくなることがわかります。 16-4 = 12 よりも、h = √ 12 = 3.5 cm に近くなります。
ヴィズナチェンニャ。 ビチナエッジ- これはトリクトゥニクであり、1つのクトがピラミッドの頂上にあり、その反対側がスタンドの側面と接触します(リクトニク)。
ヴィズナチェンニャ。 サイドリブ- これらは側面の反対側です。 ピラミッドには、波状の尾と同じ数の肋骨があります。
ヴィズナチェンニャ。 ピラミッドの高さ- ピラミッドの頂上から底辺に下る垂線。
ヴィズナチェンニャ。 崇拝者- これはピラミッドの側面に垂直で、ピラミッドの頂上からスタンドの側面に向かって下降します。
ヴィズナチェンニャ。 斜めレチン- これはピラミッドの頂点とスタンドの対角線を通る平面を持つピラミッドのクロスバーです。
ヴィズナチェンニャ。 正しいピラミッド- これはピラミッドで、ベースは通常の豊かなボディであり、高さはスタンドの中心まで下がります。
ピラミッドの被覆と表面積
式。 ピラミッドの練習底面積と高さまで:
ピラミッドの力
すべてのサイドリブが等しいため、杭はピラミッドの底部の周りに記述でき、スタンドの中心は杭の中心に近くなります。 上から下る同じ垂線がスタンド(杭)の中心を通過します。
すべてのリブが等しいため、悪臭は新しいリブの下のベースのレベルに集中します。
牛カルビは、均等なカットの底面が平らである場合、またはピラミッドの底面の周りに円を描くことができる場合、均等です。
側面が 1 つの角の下の底面まで延長されている場合、柱をピラミッドの底面に内接させることができ、ピラミッドの頂点がその中心に投影されます。
側面は一つの稜線の下で底面まで積み上げられているため、側面の頂点は水平となる。
右ピラミッドの力
1. スタンドの隅々からピラミッドの頂点を均等に取り除きます。
2. サイドリブはすべて等しい。
3. すべてのサイドリブをベースの新しいカットの下に重ねます。
4. この地域のあらゆる自然の側面を象徴するもの。
5. 平面のすべてのエッジの面積。
6. すべてのエッジは同じ二面体 (平坦) エッジを持ちます。
7. ピラミッドの周りに球を描くことができます。 記述された球の中心は、リブの中央を通る垂線の横棒の点になります。
8. ピラミッドの近くに球を刻むことができます。 内接球の中心は、エッジとベースの間のパスから現れる二等分線の横棒の点になります。
9. 内接球の中心が記述された球の中心と一致する場合、上部の平らな部分の合計は π に等しいか、またはたとえば 1 つの部分は π / n に等しく、n は数値です。ピラミッドの底辺の部分。
ピラミッドと球体の接続

ピラミッドの周囲にトーディの球体を記述することができ、ピラミッドの底部に多面体があり、その周囲に円を描くことができます(必要十分な知性)。 球の中心は、ピラミッドの側端の中央を垂直に通る平面の横棒の点になります。
単純なまたは正確なピラミッドを使用して球を記述することができます。

ピラミッドの内部二面角の二等分面が 1 点で交差する場合 (必要かつ十分)、ピラミッドに球を内接することができます。 この点が球の中心になります。
ピラミッドと円錐のリンク
円錐は、それらの頂点が交わっており、円錐の底面がピラミッドの底面に内接しているため、ピラミッドに内接されていると呼ばれます。
角錐は互いに等しいため、円錐は角錐に内接することができます。
円錐は、それらの頂点が交わることからピラミッドの記述と呼ばれ、円錐の底面はピラミッドの底面として記述されます。
角錐のすべての側面リブが互いに等しいため、角錐は角錐の周りに記述することができます。
ピラミッドと円柱の間のリンク
ピラミッドの頂点が円柱の 1 つの底面にあり、ピラミッドの底面が円柱の別の底面に内接しているため、ピラミッドは円柱に内接すると呼ばれます。
円柱はピラミッドの底面の周囲に記述できるのと同様に、ピラミッドの周囲に円柱を記述することができます。


四面体には 4 つの面、4 つの頂点、および 6 つのエッジがありますが、2 つのエッジは互いに接触または衝突しません。
皮膚の頂点は 3 つのエッジとリブで構成され、 三角カット.
四面体の頂点と近位面の中心を結ぶカットを次のように呼びます。 正四面体の中央値(GM)。
ビメディアン互いにくっついていない前立腺肋骨の中央を接続するカット(KL)と呼ばれます。
すべての二中央線と四面体の中央値は 1 点 (S) で交差します。 この場合、二中央値は半分に分割され、比率の中央値は上から 3:1 になります。


ヴィズナチェンニャ。 ゴストロクトゥナピラミッド- これは、基底面の半分以上に神格者がいるピラミッドです。
ヴィズナチェンニャ。 鈍角ピラミッド- これは、アポセムが底面の半分未満であるピラミッドです。
ヴィズナチェンニャ。 正四面体- 4 つの辺すべてを持つ四面体 - 等しい辺のトリキュール。 ヴィンは5人に1人です 正しい富裕層。 正四面体では、すべての二面体のエッジ (面の間) と三面体のエッジ (頂点の) は等しいです。
ヴィズナチェンニャ。 直四面体頂点の 3 つのリブの間に直線がある (リブが垂直である) ものを四面体と呼びます。 3つの顔が作成されます ストレートカット トライアングルカットそしてボーダーは直線のトリカット、ベースは長いトリカットです。 どの面のアポセムも、そのアポセムが置かれるベースの側面の同じ半分にあります。
ヴィズナチェンニャ。 等面体四面体側面が等しい正四面体と呼ばれるもので、底辺は正三面体です。 このような四面体には三皮境界があります。
ヴィズナチェンニャ。 四面体の直心度頂点から延長面までの高さ(垂線)がすべて一点で交わる形状を四面体といいます。
ヴィズナチェンニャ。 夜明けのピラミッドスターをベースにしたリッチフェイスと呼ばれます。

ここでは、お尻と義務の理解について見ていきます。 このようなタスクを完了するには、ピラミッド公式を知ることが絶対に必要です。

S
h - ピラミッドの高さ
裕福な人が代わりになるかもしれない。 しかし、ほとんどの場合、心の中のЄДІ言語に関する指示は、原則として、正しいピラミッドに関するものです。 以下の当局の 1 つを思い出してください。
正しいピラミッドの頂上がベッドの中心に投影されます
規則的な三皮錐、三皮錐、六角錐の投影図に驚嘆してください (トップビュー):

ピラミッドの問題に関連する問題を整理できたことは間違いありません。エリアを見てみましょう:
27087. 各辺の辺が 1 に等しく、高さが 3 の平方根に等しい、正三角形のピラミッドの体積を求めます。


S- ピラミッドの底辺の面積
h- ピラミッドの高さ
私たちは、正しいトライカットであるピラミッドの底の面積を知っています。 速度の公式によると、三脚の面積は、隣接する辺の半分とそれらの間の正弦に等しくなります。これは、次のことを意味します。


タイプ: 0.25
27088. 正三角錐の高さ、底面の辺が 2、対応する 3 の根を求めます。

ピラミッドの高さやベッドの特性などの概念は、次の式に関連しています。

S- ピラミッドの底辺の面積
h- ピラミッドの高さ
彼自身、スタンドであるトリクトニクの側面からスタンドの面積を知ることができると語った。 練習せずに指定値を知ると高さがわかります。
正方形の面積を見つけるには、速度の公式を使用します。トリクプータの面積は、隣接する辺の間のカットの正弦によって隣接する辺の半分に等しくなります。これは、次のことを意味します。

この方法を使用して、これらの値を式に代入することで、ピラミッドの高さを計算できます。

高さは3つくらいあります。
タイプ: 3
27109. 正平行錐では、高さは 6、辺の高さは 10 です。これらを見つけることが義務付けられています。
ピラミッドのコストは次の式を使用して計算されます。

S- ピラミッドの底辺の面積
h- ピラミッドの高さ
その高さは私たちにとって馴染みのあるものです。 ベースの面積を知る必要があります。 正しいピラミッドの頂上がそのベッドの中心に投影されていると推測してみましょう。 正半円錐の底辺は正方形です。 その対角線を知ることができます。 ストレートカットのトリカット (青で表示) を見てみましょう。

カットは、正方形の中心と、正方形の対角線の半分に等しいこちら側の点 B を結びます。 この区間はピタゴラスの定理を使用して計算できます。
したがって、BD = 16 です。正方形の面積は、正方形の面積の公式を使用して計算できます。

オッツェ:
このようにして、古代のピラミッドは作られました。

提出数: 256
27178。通常の四角錐では、高さは 12 ですが、200 にもなります。このピラミッドの側端を見つけます。

ピラミッドの高さも表示されます。これは、ピラミッドの底辺である正方形の面積を見つけることができることを意味します。 正方形の面積がわかれば、その対角線もわかります。 直線状のトライカットをさらに詳しく見てみると、ピタゴラスの定理によれば、横方向のエッジは数えられます。

正方形(ピラミッドの底面)の面積がわかります。

正方形の対角線を計算してみましょう。 したがって、その面積は 50 に等しいため、ピタゴラスの定理によれば、辺は 50 i の根に等しくなります。
点 O は、対角線 BD をある方向に分割します。これは、直腸三皮脚 OB = 5 を意味します。
このようにして、ピラミッドの古代の側端が何であるかを計算できます。
バージョン: 13
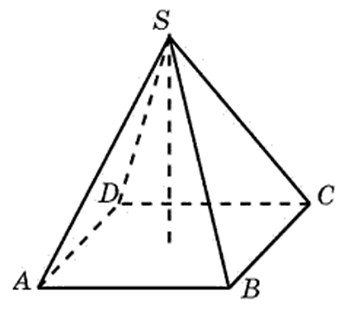
245353. 赤ちゃんに表示されているピラミッドの体積を求めます。 その基部は茂みであり、その側面は垂直であり、側面リブの1つは基部と底面の平面に対して垂直です。

すでに何度も述べたように、ピラミッドのコストは次の式を使用して計算されます。

S- ピラミッドの底辺の面積
h- ピラミッドの高さ
側端は古代の 3 つの底面に垂直であり、これはピラミッドの高さが古代の 3 つであることを意味します。 ピラミッドを想像してみてください - これは豊かな茂みであり、その領域は古代です。
この順序で:

バージョン: 27
27086。ピラミッドの底部は、辺 3 と 4 を持つ直腸です。これは 16 と同じです。このピラミッドの高さを求めます。
ピラミッドはリッチフェイスと呼ばれ、そのベースはかなりリッチな側面であり、すべてのフェイスは横方向の頂点、つまりピラミッドの頂点を持つトリカットです。
ピラミッドは体積を表す図形です。 これを行うには、多くの場合、地域だけでなく、地域についても知る必要があります。 ピラミッドの公式は非常に簡単です。
![]()
ここで、S はスタンドの面積、h はピラミッドの高さです。
身長ピラミッドはストレートと呼ばれ、頂点から直線エッジの下の底辺まで下がっています。 明らかに、ピラミッドの体積を知るためには、底辺にどのような構造があるのかを把握し、その面積を拡大し、ピラミッドの高さを調べ、その義務を知る必要があります。 ピラミッドのお尻を見てみましょう。
コマンド: 正しいピラミッドが与えられます。 
スタンドの側面 a = 3 cm、すべての側面リブ b = 4 cm ピラミッドの体積を求めます。
まず、拡大するにはピラミッドの高さが必要であることは明らかです。 これはピタゴラスの定理によって知ることができます。 そのためには対角線の半分、より正確には半分が必要になります。 三皮木の表裏がわかれば高さがわかります。 穂軸の場合、対角線がわかります。 
値を式に代入してみましょう。 ![]()
高さ h mi は、d とエッジ b の助けからわかります。 

今、私たちは知っています
正三立方体を基本とし、その他の面は正等辺三立方体で表される藻類面を「藻類面」と呼びます。 三尖錐台このようなピラミッドは四面体とも呼ばれます。
どのような数字が形成されるかがわかるように、正しいピラミッドには権威はありません。
- すべての側は基本的に互いに互換性があり、それは正しいトリクトニクによって表されます。
- ピラミッドのすべての辺は互いに等しい。
- スキンエッジが破片を除去します 等大腿トリカットリブが等しく、ベースが等しい場合、スキンエッジの面積は同じであると言えます。
- すべての上反面カットは平面の底部にあります。
スタンドとバレルの面積の合計として保険が適用されます。 側面と底面のどちらかの面積を拡大する方法もわかります。 三皮ピラミッドの公式も、それが形成されるトリキュビチンの力に由来しています。
![]()
スタンドの面積は、次の式を使用して保険可能です。 
3ピースピラミッドの構造のお尻を見てみましょう。
3 つの部分からなるピラミッドを考えてみましょう。 底面の辺の高さは a = 2 cm、高さの高さは h = 2√3 です。 指定された花崗岩の体積を求めます。
穂軸については、立つべき領域がわかっています。 指定されたデータを次の式に代入します。 
これで、三皮錐体の構造の意味がわかりました。 ![]()
平らな三皮錐体を拡大するには、短縮された式を使用することもできます。 これは、底辺の面積と高さを示しており、式は、底辺の面積の 3 分の 1 からピラミッドの高さまでのようなものになります。
この公式を勉強するときは、近道と近道を厳密に守ることが重要です。 1 つの小さな調整が間違った結果につながる可能性があります。 一般に、正しい三皮錐体の体積を知ることは非常に簡単です。



