Podajte razumevanje problema
Problem je bolj teoretična in praktična hrana, ki jo je treba opravičiti, virishennya; v znanosti obstaja nadenostavna situacija, ki glede na nasprotna stališča pri razlagi ali stvari, predmeti, procesi in zahtevajo ustrezno teorijo in rešitev. Pomemben premislek o uspešnem ločevanju češenj. težave in služi njeni pravilni nastavitvi.
Kaj menite o izbiri?
Najprej poglej spodaj možne možnosti Za rešitev problema je potrebno, da referent identificira indikacije, ki bodo uporabljene za primerjavo alternativ in izbiro najboljše. Indikatorji Qi se običajno imenujejo izbirna merila.
Kaj je optimalna rešitev?
V idealnem primeru je mogoče identificirati vse možne alternativne načine reševanja problema, le tako je rešitev lahko optimalna. Kerivnik pa v praksi nima takšnih zalog znanja in časa, da bi oblikoval in ovrednotil koži prijazno alternativo. Zato smrad ni optimalen, ampak doseči prijazno, prijetno možnost, ki vam omogoča, da rešite problem, in vam pomaga pri nesprejemljivi alternativi izbirnemu merilu, ki je bilo imenovano na prejšnji stopnji.
Vodja linijskega programiranja (LLP) za najvišjo (ali najmanjšo) vrednost linearne funkcije na razkošni bogati mnogoterosti.
Simpleksna metoda je enaka metoda reševanja problemov linearnega programiranja. Bistvo metode temelji na pomembnosti dovoljenega načrta storža in v nadaljevanju na pol poti doseči največjo (ali najmanjšo) vrednost ciljne funkcije v tem večplastnem bogatem množitelju oziroma razložiti nedoslednost naloga.
Oglejmo si prihajajoče linijsko programiranje v kanonični obliki:
| (1) |
| (2) |
| (3) |
Metoda na osnovi kosov
Ker je bilo za nalogo, napisano v kanonični obliki, dodeljeno več kot sredina vektorjev v stolpcih matrike Aє m enojni in linearno neodvisni, lahko navedete referenčni načrt brez sredine. Vendar pa so za bogate naloge linearnega programiranja, zapisane v kanonični obliki in lahko podpirajo načrte, srednji vektorji v matriki A ne začenjaj m sam in linearno neodvisen. Oglejmo si naslednjo nalogo:
Naj bo treba poznati maksimum funkcije
za ume
de perche n elementi so nič. Spremembe ![]() se imenujejo umetne. Vektorji
se imenujejo umetne. Vektorji
  | (28) |
za vzpostavitev takšnih naslovov kot kosovne osnove m-svetovni vektorski prostor.
Oskílki naloga je razširjena na osnovni načrt, njena rešitev je mogoče poznati metodo simpleksa.
Izrek 4. Kot optimalni načrt ![]() razširjena nastavitev (24)-(26) vrednosti menjave kosov
razširjena nastavitev (24)-(26) vrednosti menjave kosov ![]() , potem
, potem ![]() ê optimalen načrt nalog (21)-(23).
ê optimalen načrt nalog (21)-(23).
Na ta način, kot so v najdenem optimalnem načrtu za razširjeno nalogo, so vrednosti kosovnih sprememb enake nič, potem se optimalni načrt za razširjeno nalogo odvzame. Naredimo poročilo o pomembni rešitvi razširjene naloge.
Vrednost ciljne funkcije za referenčni načrt (27):
Ugotavljamo, da F(X) in so sestavljeni iz dveh neodvisnih delov, od katerih je eden deponiran v M, in insha - ní.
Po izračunu F(X) da se njihove vrednosti in izhodni podatki razširjene naloge vnesejo v tabelo v simpleksu, kot je prikazano zgoraj. Edina razlika je v tem, da tabela nadomesti eno vrstico večje, manjše enostavne tabele. Ko ti ( m+1) vrstica je postavljena s koeficienti, ki se ne maščujejo M in v ( m+2)-ta vrstica − koeficienti pri M.
Pri prehodu iz enega referenčnega načrta v drugega je osnova vnesti vektor, ki je najprimernejši za absolutna vrednost negativno število ( m+2) vrstice. Kos vektorja, nima smisla ponovno uvajati osnove iz baze. Pri prehodu na drug referenčni načrt se lahko izkaže, da ne bo nobenih izključitev kosovnih vektorjev iz osnove. Simpleksna tabela se spreminja pri prehodu z enega referenčnega načrta na naslednjega, spreminja se v skladu s strogimi pravili metode simpleks (div. višje).
Iterativni postopek poteka v skladu z m+2 po vrsti za tiho jelko, pokie elementi m+2 vrstici za spremembo ![]() ne postanejo nevidni. Ko je vsaka posamezna sprememba izključena iz osnove, je načrt znanja razširjene naloge skladen s trenutnim osnovnim načrtom izhodne naloge.
ne postanejo nevidni. Ko je vsaka posamezna sprememba izključena iz osnove, je načrt znanja razširjene naloge skladen s trenutnim osnovnim načrtom izhodne naloge.
m+2 vrstici x 0 negativno, potem ni rešitve.
No, niso vse spremembe kosov izklopljene iz osnove tega elementa m+2 vrstici x 0 do nič, potem je referenčni načrt izhodne naloge virogenim in je osnova vsaj eden od vektorjev baze kosa.
Praviloma je treba odstraniti kos posameznih vektorjev in jih vključiti v osnovo kosa.
Koliko ur ponovitev m+2 vrstica ni več maščevanja za negativne elemente, potem se bo ponovitveni proces nadaljeval z m+1 Zaporedoma so doki našli optimalen načrt za razširitev naloge in razkrili nedoslednost problema.
Tako postopek reševanja problema linearnega programiranja (21)-(23) z metodo kosovne osnove vključuje naslednje glavne faze:
- Zložite razširitev naloge (24) - (26).
- Spoznajte osnovni načrt razširjene naloge.
- Metoda Vikoristovuyuchi simplex vključuje delne vektorje iz osnove. Posledično poznati osnovni načrt izhodne naloge ali odpraviti nedoslednost.
- Vykoristovuyuchi poznavanje osnovnega načrta ZLP (21) - (23), ali poznate optimalen načrt vihіdnoї nalog, ali namestite njeno nerazvjaznіst.
Za spletno reševanje problemov linearnega programiranja uporabite kalkulator
Glavna naloga linearnega programiranja (OZLP) je formulirana na naslednji način - poznati spremembo naloge x 1 , x 2 , ..., x n, da zagotovimo ekstrem ciljne funkcije
Dopustne rešitve (načrt) problema linearnega programiranja (ZLP) imenujemo karkoli n- miren vektor X=(x 1 , x 2 , ..., x n), ki zadovoljuje sistem z mejo enakosti in nepravilnosti. Anonimni sprejemljivi jeziki D.
Optimalno rešitev (načrt) problema linearnega programiranja imenujemo takšna dopustna rešitev, za katero je funkcija Z(X) dosežejo ekstrem.
Lahko se vidi kanonični problem linearnega programiranja (KZLP).
 (1.2)
(1.2)
Vaughn v_drіznyaêtsya víd OZLP tim, njen sistem je obmezhen je samo sistem enak in vse spremembe so nenegativne.
Prenos OZLP v kanonično obliko ZLP:
Za zamenjavo naloge minimizacije z nalogo maksimizacije (sicer je naloga maksimizacije naloga minimizacije), pomnožite ciljno funkcijo z “-1” in izračunajte maksimum (minimum) maksimizacijske funkcije;
Če je sredina meje neenakomerna, potem s pomočjo pošiljke dodatnih nevidnih sprememb x n +1 ≥ 0
neenakomernost a jaz 1 x 1 +…+a v x n≥ b zamenja me ljubosumje a jaz 1 x 1 +…+a v x n+ x n+1 = b jaz ,
neenakomernost a jaz 1 x 1 +…+a v x n≤ b zamenja me ljubosumje a jaz 1 x 1 +…+a v x n+ x n+1 = b jaz;
Sprememba Yakshcho deyaka x k Če meje po znaku nimate, se le-ta nadomesti (za celotno funkcijo in v obstoječih objektih) z razliko med obema z novimi nevidnimi spremembami: x k = x" k – x” k , de x" k ≥ 0. x” k ≥ 0.
Grafična metoda reševanja ZLP iz dveh nevidomij
ZLP іz dva nevіdomimi maê vyglyad:

Metoda temelji na izvedljivosti grafičnega prikaza območja sprejemljivih rešitev in pomembnosti povprečja optimalne rešitve.
Območje dovoljenega rozv'yazkív (ODR) naloge je nabreknjeno s hroščem in bo kot peretina (slan del) območij rozv'yazkіv dermalne razdražljivosti meje problema.
Območje rozvyazannya živčnost a jaz 1 x 1 +a jaz 2 x 2 ≤ b i je eden od dveh napívploschin, na yaki naravnost a jaz 1 x 1 +a jaz 2 x 2 = b jaz koordinatna ravnina. Za označevanje območja rešitve, kot iz dveh ravnih ravnin, zadostuje koordiniranje katere koli točke, ki ne leži na ravni črti, ki se deli na neravnine:
Če je neenakost poštena, potem je območje rešitve ravno območje, ki maščuje to točko;
Če neenakost ni pravična, je območje rešitve ravno območje, da ne bi maščevali točke.
Za znahodzhennya sprejemljivega obsega optimalne rešitve so črte vicorirane.
Ravna črta se imenuje ravna črta h 1 x 1 +h 2 x 2 = l, de l= konst Linije brkov so med seboj vzporedne.
Gradient ciljne funkcije grad Z(X) nastavi normalni vektor C = (c 1 , c 2) linija rivnya. Glavna funkcija na črtah črte raste, saj se črte črte premikajo po ravni črti normale in manj - po ravni črti.
Referenčna črta se imenuje črta reke, kot če bi želel uporabiti eno središčno točko iz ODR in glede na razdaljo do tega ODR biti v eni od ravnin. Naloga ODR ne sme biti več kot dve referenčni črti.
Optimalna rešitev ZLP je ležanje na nosilni ravni liniji na vrhu bagatokutnika ODR. ZLP ima lahko le eno rešitev, da gre referenčna črta skozi eno temensko točko ODR, neosebna rešitev, kot da gre referenčna črta skozi rob bagatokutnika ODR. ZLP ni rešitev, tako kot ODR je prazna brezosebnost (če je sistem nekompatibilen) in tako kot ODR ni vezan na ekstrem (ciljna funkcija ni vezana).
Algoritem za grafično metodo risanja ZLP iz dveh neznank:
Takojšnji ODR.
Inducirajte normalni vektor C = (c 1 , c 2) ta vrstica h 1 x 1 +h 2 x 2 = 0, da poteka skozi koordinatni storž in pravokotno na vektor W.
Premaknite črto poravnave na referenčno črto na ravni črti vektorja W pri obratu pri max, in na ravni liniji - pri obratu pri min.
Tudi če je črta premaknjena neposredno na ekstrem ODR, gre v nekonsistentnost, potem ZLP ni mogoče rešiti z neobveznostjo ciljne funkcije.
Če je lahko ZLP optimalna rešitev, potem je za ta namen odlična rešitev poravnava ravnih črt, ki mejijo na ODR in tvorijo pike na referenčni črti. Če je ekstrem dosežen na dveh vrhovih, potem je LLP lahko neosebna odločitev, da leži na robu ODR, obdan s točkami vrha tsimi. Včasih se izračunajo koordinate obeh vrhovnih točk.
Izračunajte vrednost ciljne funkcije na ekstremni točki.
Simpleksna metoda za reševanje VŽU
Simpleksna metoda temelji na naslednjih določbah:
ODR problema linearnega programiranja je bomo razpršili z množiteljem s končnim številom vrhovnih točk;
Optimalne rešitve VŽU so temenske točke ODR. Kutoví točka ODR algebraično predstavlja deyakí osnovno (referenčno) rešitev sistema meja ZLP.
Osnovne (nosilne) rešitve PLP imenujemo take dopustne rešitve X 0 =(x 10 , x 20 , ..., x m 0, 0, ... 0)
Neničelne koordinate x 10 , x 20 , ..., x m 0 raztopina X 0 imenujemo osnovne spremembe, koordinate rešitve, ki se izgubijo X 0 - brezplačne spremembe. Število podanih ničelnih koordinat referenčne rešitve ne more biti večje od ranga r sistem obrobnih PLP (število linearno neodvisnih enačb v sistemu obrobnih PLP). p align="justify"> Pomembno je omeniti, da je sistem mejnega VŽU sestavljen iz linearno neodvisnih ravni, tj. r = m.
Smisel simpleksne metode gre neposredno v ciljno usmerjen prehod od ene referenčne rešitve ZLP do naslednje (to je od ene od vrhov ODR do naslednje) neposredno do ekstrema in gre do zaporedje korakov:
poznati osnovo rešitve;
spremeniti prehod iz ene referenčne rešitve v drugo;
Odločite se o merilu za doseganje optimalne rešitve za razvoj visnovi o veljavnosti rešitve.
Wicoon algoritemSimpleksna metoda ZLP
Algoritem metode simpleksa zdíysnyuê prehod iz ene referenčne rešitve ZLP na naslednjo neposredno do ekstrema ciljne funkcije.
Naj bo ZLP podan v kanonični obliki (1.2) in vikonano
b i ≥ 0, jaz=1,2,…,m, (1.3)
spіvvіdnennia (1.3) se lahko vikonati z množenjem vіdpovіdne vіnnіannya z "-1" v različnih negativnosti b jaz. Pomembno je tudi, da je sistem enakosti v razdelkih problema (1.2) linearno neodvisen od tega ranga r = m. Za koga lahko vektor referenčne rešitve m neničelne koordinate.
Pojdimo ven iz pisarne (1.2), (1.3) se spomnimo, de osnovne spremembe x 1 , x 2 , ..., x m x m + 1 , x m + 2 , ..., x n
 (1.4)
(1.4)
Na podlagi tsikh spіvvіdnoshen zbuduєmo tabelo 1
Tabela 1

Tabela 1 se imenuje simpleks tabela. Brki nadaljnje preoblikovanje pov'yazani іz zminami zmіstu tsієї tabele.
Algoritem hmetoda implex:
1. V preostali vrstici Z Simpleksne tabele imajo najmanjši pozitivni element za nalogo pri min (najmanjši negativni element za problem pri maks.), crim prostega člana. Stovpets, ki podpira ta element, se imenuje ločena zgradba.
2. Izračunajte število razširitev glavnih članov na pozitivne elemente divizijske strukture (simpleksna razširitev). Če želite vedeti najmanj teh simplex - vídnosin, vono vídpovіdaє razdіlnіy zdatností.
3. Samostojna stavba je na obodu samostojne stavbe in samostojne stavbe.
4. Če je papalina enaka za velikost simpleksa - vídnosin, potem izberite, ali je od njih. Te veljajo za pozitivne elemente preostale vrstice simleksa - tabel.
5. Po pomenu ločenega elementa pojdite na naslednjo tabelo. Nevidne spremembe, ki spreminjajo velikost stavbe in konstrukcije, spreminjajo mesta. Hkrati osnovna sprememba postane brezplačna sprememba in navpaki. Simplex - tabela se preoblikuje na naslednji način (tabela 2):
Tabela 2

6. Element tabele 2, ki je podoben porazdelitvenemu elementu tabele 1, je pomemben dejavnik pri porazdelitvi elementa.
7. Elementi vrstice tabele 2, ki ustrezajo elementom razporeditve stavbe v tabeli 1, potekajo vzdolž linije ustreznih elementov v tabeli 1 do elementa razporeditve.
8. Elementi tabele 2, ki ustrezajo elementom razporeditve gradbenih zmogljivosti tabele 1, potekajo vzdolž črte pod ustreznimi elementi v tabeli 1 do ločenega elementa in so vzeti z nasprotnim predznakom.
9. Drugi elementi so izračunani za pravilo pravokotnika: misli v obliki pravokotnika na mizi 1, od katerih en vrh poteka z ločenim gradbenim elementom (Re), in insha - z elementom, o katerem se šalimo; Pomembno je, da element v novi tabeli 2 skozi (He), in element, ki stane enako prostora v stari tabeli 1 - skozi (Ce). Drugi dve točki A in B dodajata lik pravokotniku. Isti zveneči element Ne iz tabel 2 dovnyu Ne \u003d Ce - A * B / Re.
10. Kriteriji optimalnosti. Takoj ko zagledamo tabelo, v nadaljevanju vrstice v nalogi za min so vsi elementi negativni (v nalogi za max vsi pozitivni elementi), pomembno je, da je ekstrem znanja. Optimalna vrednost ciljne funkcije je enaka variabilnemu členu serije Z, optimalno rešitev pa določajo variabilni členi z osnovnimi spremenljivkami. Vrednosti gorčice so enake nič.
11. Če so vsi elementi negativni za nadrejenega partnerja, potem ni rešitve (minimum ni na voljo).
Rešitev po delih LLP
Algoritem simpleksne metode je fiksen, saj je bil viden kot glavna rešitev VŽU, to je, da je bil zaključek VŽU (1.2) priveden v obliko (1.4). Metoda po delih spodbuja postopek za indukcijo takšne referenčne rešitve.
Metoda delne osnove temeljev o uvedbi kosovnih sprememb podlage l 1 , l 2 ,…, l m
 (1.5)
(1.5)
morda se je buti spremenil v pogled
 (1.6)
(1.6)
Sistema (1.5) in (1.6) bosta enakovredna kot vsi l jaz nastavite na nič. Tako kot prej skrbimo, da vse b jaz ≥ 0. Da bi pri jaz dodano 0, je naša napaka, da nalogo predelamo tako, da imamo osnovno spremembo l jaz šel na vílní zminnі. Takšen prehod lahko generira simpleksni algoritem z uporabo metode dodatne ciljne funkcije
F(l) = l 1 + l 2 + ... + l m = d 0 – (d 1 x 1 +d 2 x 2 +…+d n x n). (2,7)
Oglejte si preprosto tabelo za to metodo

Zaporedna enostavna tabela se preoblikuje glede na namen funkcije F(l) Do odvzema referenčne raztopine. Osnova rešitve je najdena, če je najden napredni kriterij: F(l) = 0 in vsi deli so spremenjeni pri jaz prevedeno iz vílní zminnі. Uporabimo preproste tabele, da ustvarimo vrstico za F(l) in stolpce za pri jaz in spremenite nalogo za zunanjo ciljno funkcijo Z(x) Dokler ni dosežena optimalna rešitev.
Izrek 4.1. Tudi če naloge linearnega programiranja do maksimuma (minimuma), če je samo en vektor misli, je ocena porazdelitve po osnovi nedegenerirane referenčne rešitve negativna (pozitivna), potem je referenčno rešitev mogoče razširiti, t.j. lahko poznate novo referenčno rešitev, ki ima večjo (manjšo) funkcijo.
Prinašanje. Pojdimo proti ideji do maksimuma, kot da ne moremo razviti osnovne rešitve,  , da je ocena porazdelitve trenutnega vektorja umov negativna (
, da je ocena porazdelitve trenutnega vektorja umov negativna (  ).
).
Preidimo na novo referenčno rešitev, v bazo vnesemo vektor i in vklopimo vektor iz baze. Za koga mislite, da povečanje funkcije zdravih
Rešitev ni virogena, zato parameter , ki je izračunan po formuli (4.5), štejemo za nič (> 0). Oskílki > 0,  , potem
, potem
Prav tako bo vrednost ciljne funkcije na novi referenčni rešitvi večja, na prvi nižja.
Manj analogen je dokaz za managerja.
Zadnji 1(Umov najbližji pristop k optimalni rešitvi). Za največjo spremembo ciljne funkcije pri razširitvi referenčne rešitve je treba izbrati vektor, ki je izpeljan iz baze (s št. l), ki se vnese v osnovo (s številko k), pretresite misli:
- pri nalogi maksimalno  ; (4.10)
; (4.10)
– pri upravniku za minimalca  . (4.11)
. (4.11)
V poenostavljeni različici izbire vektorja, ki je vnesen v osnovo, je mogoče izvesti um:
- pri nalogi maksimalno  ; (4.12)
; (4.12)
– pri upravniku za minimalca  . (4.13)
. (4.13)
Ta različica na začetku nove podporne rešitve bo zvenela zmagovito na otvoritvah na EOM.
Zadnji 2(Predznak optimalnosti referenčne rešitve). Osnova rešitve problema linearnega programiranja do maksimuma (minimum) je optimalna, zato za kateri koli vektor umov ocena postavitve na podlagi rešitve podpore ni mogoča (nepozitivna), tj. .
- pri nalogi maksimalno  ; (4.14)
; (4.14)
– pri upravniku za minimalca  . (4.15)
. (4.15)
Prav, tako je Z(x) ![]() ,
,  ,
,  , potem
, potem
to je optimalna rešitev. Za upravitelja je minimalno dokazilo podobno.
Zadnji 3(Znak enotnosti optimalne rešitve). Optimalna rešitev problema linearnega programiranja je edina, zato je za kateri koli vektor umov, da ne vstopi v osnovo, ocena vložka enaka nič, tj.
Tukaj je navedeno, da osnova optimalne rešitve vključuje prvo m vektor_v.
Vodenje 4(Predznak baze neskončnega množitelja optimalnih rešitev). Vodja linearnega programiranja lahko nima optimalne rešitve, če pa želi enega od vektorjev umov, ki ni vključen v osnovo optimalne rešitve, je ocena enaka nič.
$ k Î { m+1,m+2, ..., n}:  . (4.17)
. (4.17)
Zadnjih 5(Znak prisotnosti optimalne rešitve skozi neobskurnost ciljne funkcije). Ni rešitve za problem linearnega programiranja z nepogajanjem ciljne funkcije, kot tudi iz vektorja umov z oceno, da bi prekrili znake optimalnosti, srednje koeficiente postavitve glede na osnovo referenčne raztopine niso pozitivne, tj.
Univerzalna metoda reševanja problemov LP se imenuje simpleksna metoda. Zastosuvannya tsgogo i yogo najpogosteje uporabljena modifikacija - dvofazna simpleksna metoda.
Z grafično metodo je naloga LP in praktično iz brezosebnih vozlišč, ki ležijo med neosebnimi rešitvami sistema nepravilnosti, izbrala takšno vozlišče, v katerem je vrednost funkcije dosegla maksimum (minimum). V času sprememb je metoda popolnoma znanstvena in omogoča hitro iskanje rešitve problema.
Ker obstajajo tri in več pomembnih nalog, resnične gospodarske naloge pa so enake, je pomembno jasno opredeliti področje rešitve sistema obmezhen. Torej zavdannya prisežem za pomoč simpleksna metoda chi po metodi naknadnega polipšena. Ideja metode je preprosta in podobna žaljivi.
Za prvim pravilom je primarni podporni načrt (deyak je vrh območja meje). Pereviryaetsya, chi je načrt je optimalen. Če je tako, potem je naloga končana. Če ne, potem gremo na drug skrajšan plan - na naslednji vrh. Vrednost ciljne funkcije v tem načrtu (na vrhu) je očitno krajša, nižja v sprednjem delu. Algoritem za prehod je ustvarjen s pomočjo neke vrste izračuna, ki ga je mogoče ročno zapisati v pregledno tabelo preproste tabele . Od končnega števila oglišč, potem za končno število krokov pridemo do racionalne rešitve.
Oglejmo si metodo simpleksa za specifično uporabo načrta naročanja.
Še enkrat, spoštljivo je, da se lahko metoda simpleksa uporabi za izboljšanje kanoničnih nalog LP, kar kaže na poseben videz, tako da so osnova, pozitivni desni deli in celoštevilska funkcija izraženi z nebazičnimi spremembami. Če naloga ni prikazana v posebnem pogledu, boste potrebovali dodatne podrobnosti, o katerih bomo govorili kasneje.
Oglejmo si načrt načrtovanja modifikacije, vnaprej uvedemo model in ga cepimo v poseben videz.
Vodja.
Za pripravo jedi AMPAKі pri skladišče lahko sprejme več kot 80 sirovini trochs. Zakaj kuhati virobo AMPAK obarvana dva enojna in virobi pri- En sam sirovini. Prihodnost je treba načrtovati tako, da bo zagotovljen največji dobiček, torej AMPAK je treba pripraviti največ 50 kosov in pri- Ne več kot 40 kosov. Še, da prihodek od prodaje enega AMPAK- 5 rubljev in pri- 3 rub.
dajmo matematični model, vedoč za X 1 število virobiv A v načrtu, X 2 - število izbir pri. Potem bo sistem videti takole:
x 1 ≤50
x2 ≤40
2x1 +x2 ≤80
x 1 ≥0, x 2 ≥0
5x1 +3x2→maks
Nalogo pripeljemo do kanoničnega videza z dodatnimi spremembami:
x 1 + x 3 =50
x2 +x4 =40
2x1+x2+x5=80
x 1 ≥0, x 2 ≥0
5x1 +3x2→maks
-F = -5x1 - 3x2 → min.
Tse zavdannya ima lahko poseben pogled (od podlage desni deli niso vidni). To je mogoče storiti s preprosto metodo.
jazstopnja. Zapišite nalogo v simpleks tabelo. Med sistemom problemov (3.10) in simpleks tabelo obstaja ujemanje ena proti ena. Ryadkіv stіlki stіlki, sіlki іvnosti і sistemí obmezhen, in stovptsіv - stylki, sіlki vіlnyh zminnyh. Osnovne spremembe zapolnijo prvo vrstico, vilni - zgornjo vrstico tabele. Spodnja vrstica se imenuje indeks, koeficienti pa se zapišejo za novo s spremembami v funkciji. Na desnem spodnjem polžu je zapisana 0, ker ni funkcije prostega člena; če є, potem pišemo yogo іz z nasprotnim znakom. Na istem mestu (v spodnjem desnem kotu) bo vrednost ciljne funkcije, tako da se bo, ko greste iz ene tabele v drugo, povečala za modulo. Tudi naš sistem mej je potrjen s tabelo 3.4 in lahko nadaljujete na drugo stopnjo rešitve.
Tabela 3.4
|
osnova |
prost |
||
IIstopnja. Ponovna potrditev optimalnosti osnovnega načrta.
Tsya tabela 3.4 potrjuje ofenzivni podporni načrt:
(X 1 , X 2 , X 3 , X 4 , X 5) = (0, 0, 50, 40, 80).
Vílnі zminní X 1 , X 2 odjava 0; X 1 = 0, X 2 = 0. In osnovne spremembe X 3 , X 4 , X 5 sprejeti vrednosti X 3 = 50, X 4 = 40, X 5 \u003d 80 - število brezplačnih članov. Vrednost ciljne funkcije:
-F = - 5X 1 - 3X 2 = -5 0 - 3 0 = 0.
Naša naloga je, da ponovno premislimo, ali je podani osnovni načrt optimalen. za kar je treba pogledati čez indeksno vrstico - vrstico ciljne funkcije F.
Možne različne situacije.
1. Kazalo F- Obstaja vrsta negativnih elementov. Otzhe, načrt je optimalen, lahko napišete naloge. Ciljna funkcija je dosegla svojo optimalno vrednost, ki je enaka številu, ki stoji na desnem spodnjem pregibu, vzeto z nasprotnim predznakom. Preidimo na stopnjo IV.
2. V indeksni vrstici, če želite en negativen element, v stolpcu ni pozitivnih. Todi robimo visnovok za tisto, kar ima namensko funkcijo F→∞ neomejeno spreminjanje.
3. V indeksni vrstici je negativen element, v stolpcu pa en pozitiven element. Nato preidemo na naslednjo stopnjo III. popravite tabelo, slikajte referenčni načrt.
IIIstopnja. Zaključek osnovnega načrta.
3 negativni elementi indeksa F- Vrstice so izbrane tako, da so največje po modulu, imenujemo jih najbolj raznolike in pomembne "".
Za izbiro druge zgradbe je potrebno izračunati število elementov skupine prostih članov samo prej pozitivno elementi ločene strukture. Izberite med otrimanih vídnosin minimalno. Vidpovidny element, ki doseže minimum, se imenuje ločena zgradba. Vidimo ga lahko s kvadratom.
Na zadnjici element 2 - virishal. Vrstica, ki ustreza temu elementu, se imenuje tudi ločena vrstica (tabela 3.5).
Tabela 3.5

Če izberemo drugo zgradbo, si prizadevamo spremeniti tabele v skladu s pravili:
1. V novi tabeli takšnih razširitev, kot prej, se spremembe v porazdelitvi zgradb in stovptsya spreminjajo po mestih, kar potrjuje prehod na novo osnovo. Naš primer ima: X 1 vnesite na podlagi, namestnik X 5, kako priti ven iz osnove in zdaj je brezplačno (tabela 3.6).
Tabela 3.6
2. Na mestu razdelitve objekta elementa 2 je zapisana številka ½.
3. Elementi samostojne stavbe se delijo na samostojni element.
4. Elementi samostojne zgradbe so deljivi na samostojni element in zapisani z nasprotnim predznakom.
5. Za zapolnitev elementov tabele 3.6, ki so izpuščeni, jih je treba spremeniti po pravilu pravokotnika. Naj želim popraviti element na presledku 50.
Zato je ta element misli površen, znano je, da je resničen, vidno je, da je resničen elementov, ki so na drugi diagonali pravokotnika, ki je viishov. Maloprodaja je razdeljena na ločen element.

Oče,. Na meglo pišemo 10, debulo 50. Podobno:
, ![]() , ,
, , ![]() .
.
Tabela 3.7

Maymo nova tabela 3.7, osnovne spremembe so zdaj spremembe (x 3 x 4 x 1). Vrednost ciljne funkcije je bila -200, to je to. spremenjeno. Za ponovni premislek o osnovni rešitvi za optimalnost je treba ponovno preiti na stopnjo II. Postopek se očitno konča, merilo zupinke je točka 1 in 2 stopnje II.
Pripeljimo naloge rozvyazannya do konca. Za to, indeksna vrstica i, ki je spremenila negativni element -½ v novo, jo imenujemo ločena zgradba i, zgіdno z III stopnje, pererahuêmo tabelo. Ko so združili modro in izbrali povprečni minimum = 40, so dodelili ločen gradbeni element 1. Zdaj je bolje, da ga spremenite s pravili 2-5.
Tabela 3.8
Po preureditvi tabel ponovno upoštevamo, da v indeksni vrstici ni negativnih elementov, torej naloga ni potrjena, osnovni načrt je optimalen.
IVstopnja. Vipisuvannya racionalna rešitev.
Ker simpleks metoda temelji na 1. odstavku druge stopnje, je treba rešitev naloge napisati v naslednjem vrstnem redu. Osnovne spremembe povečujejo vrednosti stolpcev neodvisnih članov. Naša rit X 3 = 30, X 2 = 40, X 1 = 20. Spremenil bo strošek 0, X 5 = 0, X 4 = 0. Funkcija vrednosti nastavi vrednost preostalega elementa stolpca prostih članov iz nasprotnega predznaka: - F = -220 → F= 220 F→ max, to je pravzaprav znak spremembe dvіchі. Otzhe, X* = (20, 40, 30, 0, 0), F* = 220
Pred izdajo načrta je potrebno vključiti 20 vrst AMPAK, 40 možnosti za tip B, s katerim bo presežek največji in stane 220 rubljev.
Na primer, v tem odstavku bomo narisali diagram poteka za algoritem metode simpleksa, tako da bomo natančno ponovili korake, vendar boste morda za nekatere bralce lahko prebrali, tako da puščice kažejo branje neposrednosti.
Moč nad pravokotniki v diagramu poteka bo pokazala, na kateri stopnji naj bo podtočka v isti skupini transformacij. pravilo o pomembnosti osnovnega načrta bo oblikovano v klavzuli 3.7.

Zadnjica. Virišiti začetek LP v kanonični obliki po metodi simpleksa.
f(x)=x 1 +9x 2 +5x 3 +3x 4 +4x 5 +14x 6 → min
x1 +x4 =20
x2 +x5 =50
x 3 + x 6 =30
x 4 + x 5 + x 6 = 60
x i ≥ 0, i = 1,…,6
Reči, da ima lahko naloga LP kanonično obliko, da lahko vsi obmezhennia (zločin umov nevidnosti sprememb) izgledajo kot enakosti in vsi svobodni člani neznanega. Oče, lahko ga postavimo v kanonično obliko.
Ideja metode simpleksa je podobna stopenjski. Na hrbtni strani je treba označiti deak (pochatkov) vrh bagatoedra dopustnih rešitev (na glavi dopustna osnovna rešitev). Ponovno preučimo rešitev glede optimalnosti. Če je optimalna, potem je rešitev znana; če ne, pojdite na drugo oglišče bagatoedra in ponovno obrnite optimalnost. Če pokličemo konec vrhov bagatoedra (zadnji konec meje rastline LP), za zadnje število "lopov" poznamo najmanjšo ali največjo točko. Naslednji korak je navesti, kako se vrednost ciljne funkcije spremeni (najmanjša za nalogo) in poveča (največja za nalogo) pri prehodu skozi eno točko v drugo.
Na ta način ideja metode simpleksa temelji na treh močeh problema LP.
rešitev. Da bi določili sprejemljivo osnovno rešitev, tobto. Za določitev osnovnih sprememb je treba sistem (5.6) reducirati na "diagonalni" videz. Zastosovuyuchi Gausova metoda (metoda zaporednega vključevanja nevidomih), je možno iz (5.6):
x 2 + x 1 + x 3 \u003d 40
x4+x1=20
x5 -x1 -x3 = 10
x6+x3=30
Otzhe, osnovna sprememba x 2 x 4 x 5 x 6 jim dajemo pomen, enak neodvisnim članom vodilnih vrstic: x 2 = 40, x 4 = 20, x 5 = 10, x 6 = 30,. Spremembe x 1і x 3 je neosnovno: x 1 = 0, x 3 = 0.
Imejmo razumno osnovno rešitev
x 0 = (0,40,0,20,10,30) (5,9)
Ponovno preveriti optimalnost najdene rešitve x0 Potrebno je, da ciljna funkcija vklopi osnovne spremembe (za dodatni sistem (5.8)) in inducira posebno simpleks tabelo.
Ko izklopite funkcijo spremembe, ročno zapišite naslednje:
f(x) = -7x 1 - 14x 3 +880 (5,10)
Zdaj pa za pomoč (5.8) - (5.10) dodamo tabelo cob simplex: 
V ničelni vrstici so koeficienti zapisani z vrtljivim predznakom možnih sprememb v primeru celoštevilske funkcije. Kriterij optimalnosti (za nalogo iskanja minimuma): dopustna osnovna rešitev ( x0) je optimalen, čeprav v ničelni vrstici ni večjega strogo pozitivnega števila (zmanjšajte vrednost ciljne funkcije (880)). Zakaj širiti in tako ponavljati (tabele). Elementi ničelne vrstice se imenujejo partiture stolpcev.
Tudi splošno dopustna osnovna rešitev (5.9) ni optimalna: 7>0, 14>0
.
V ničelnem stolpcu so vrednosti osnovnih sprememb. Smrad obov'yazkovo je lahko neviden (div. enako (5.7)). Od prve do četrte vrstice so zapisani koeficienti spremembe iz sistema (5.8).
torej jak x0 neoptimalen, je treba iti v naslednje oglišče bagatoedra dopustnih rešitev (za induciranje novega dbr). Za katere je potrebno poznati bistveni element in izvesti enostavno transformacijo (simpleks transformacija).
Znano je, da je spodnja vrstica prevodni element tabele, ki stoji na prečki prevodnega stolpca (stolpca z najvišjo pozitivno oceno) in prevodne vrstice (vrstice, ki označujejo najmanjši razmik elementov ničelnega stolpca). na vodilni element pozitivnega elementa).
Tabela ima 1 vodilno vrstico - tretjo vrstico in vodilno vrstico - četrto vrstico (min(40/1,30/1)=30/1) označen s puščicami, prevodni element pa s krogom. Žični element prikazuje, kakšna je osnovna sprememba x6 ga je treba zamenjati z neosnovnim x 3. Enake nove osnovne spremembe bodo x 2 x 3 x 4 x 5, in neosnovno - x 1, x 6,. Tse pomeni prehod na nov vrh bagatoedra dopustnih rešitev. Poznavanje vrednosti koordinat nove veljavne osnovne rešitve x00 potrebno bo ustvariti novo simpleksno tabelo in na njej izvesti elementarne transformacije:
a) vse elemente žične vrste razdelite na žični element, tako da žični element spremenite v 1 (zaradi enostavnosti gnezdenja);
b) s pomočjo žičnega elementa (enako 1) obrnite vse elemente žičnega stolpca na nič (podobno kot pri izklopu neznank);
Posledično se v ničelnem stolpcu spremenijo vrednosti novih osnovnih x 2 x 3 x 4 x 5(Div. Tabela 2) – osnovne komponente novega vozlišča x00(Neosnovne komponente x 1 = 0, x 6 = 0,).

Kot kaže tabela 2, nova osnovna rešitev x00 = (0,10,30,20,40,0) suboptimalen (ničelna vrstica ima neznano oceno 7). Zato bo element 1 (div. tabela 2) nova simpleks tabela, tj. nova dopustna osnovna rešitev 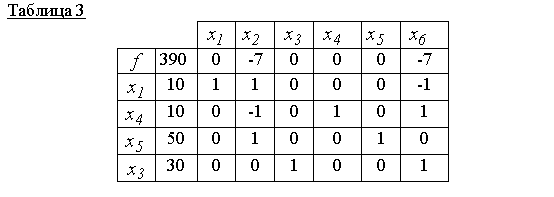
Tabela 3 prikazuje sprejemljivo osnovno rešitev x000 = (10.0.30.10.50.0) i joga je optimalna, saj v ničelni vrstici ni pozitivnih ocen. Tom f(x000)=390 je minimalna vrednost ciljne funkcije.
Predlog: x000 = (10, 0, 30, 10, 50, 0)- minimalna točka, f(x000)=390.
Pametno standardno programiranje linij
Takšno nalogo je treba vikontirati po naročenem vrstnem redu.- Poiščite optimalen načrt za neposredno nalogo:
a) grafična metoda;
b) metoda simpleks (za spodbujanje izvedljivega referenčnega načrta je priporočljiva uporaba metode po kosih). - Obvestite skrbnika.
- Poznavanje optimalnega načrta za dvojno težavo iz preproste grafične rešitve, nadomestnega uma, ki prispeva k preprostosti.
- Poiščite optimalni načrt za dvoproblemski problem po prvem izreku o dveh problemih, poiščite rezidualno simpleksno tabelo, odštejte uro primarnega problema (div. str. 1b). Ponovno razmislite o trditvi "vrednosti ciljnih funkcij stav dvojnih nalog se spreminjajo glede na njihove optimalne rešitve."
- Predložite nalogo reševanja simpleksne metode, nato pa uporabite rezidualno simpleksno tabelo dvojne naloge, da poznate optimalni načrt neposrednega problema po prvem izreku o dvojnosti. Rezultat enačite z rezultatom, odštejte po grafični metodi (razdel. str. 1a).
- Poiščite optimalni cilj rešitve:
a) grafična metoda;
b) Gomoryjeva metoda.
Možnost vrednosti funkcij celih in necelih rešitev
Hrana za samokontrolo
- Kako bo delovala preprosta tabela?
- Kako spremeniti osnovo tabele?
- Formulirajte zubikov kriterij simpleksne metode.
- Kako organizirati preoblikovanje mize?
- Koliko vrstic morate ročno odpreti tabel?



