Формула кола на координатній площині. Побудова графіків онлайн

Аналітична геометріядає однакові прийоми розв'язання геометричних завдань. Для цього всі задані та шукані точки та лінії відносять до однієї системи координат.

У системі координат можна кожну точку охарактеризувати її координатами, а кожну лінію – рівнянням із двома невідомими, графіком якого ця лінія є. Таким чином, геометрична задача зводиться до алгебраїчної, де добре відпрацьовані всі прийоми обчислень.

Коло є геометричне місце точок з однією певною властивістю (кожна точка кола рівновіддалена від однієї точки, називається центром). Рівняння кола має відображати цю властивість, задовольняти цю умову.

Геометрична інтерпретація рівняння кола – це лінія кола.

Якщо помістити коло в систему координат, то всі точки кола задовольняють одній умові - відстань від них до центру кола має бути однаковим і рівним колу.

Коло з центром у точці А та радіусом R помістимо в координатну площину.

Якщо координати центру (а; b) , а координати будь-якої точки кола (х; у) , то рівняння кола має вигляд:

Якщо квадрат радіуса кола дорівнює сумі квадратів різниць відповідних координат будь-якої точки кола та її центру, це рівняння є рівнянням кола в плоскій системі координат.

Якщо центр кола збігається з точкою початку координат, то квадрат радіуса кола дорівнює сумі квадратів координат будь-якої точки кола. У цьому випадку рівняння кола набуває вигляду:

Приклади розв'язання задач рівняння кола

Завдання. Скласти рівняння заданого кола

Рішення.
Звернемося до формули рівняння кола:
R 2 = (x-a) 2 + (y-b) 2

Підставимо значення формулу.
Радіус кола R = 4
Координати центру кола (відповідно до умови)
a = 2
b = -3

Отримуємо:
(x - 2) 2 + (y - (-3)) 2 = 4 2
або
( x - 2 ) 2 + ( y + 3 ) 2 = 16 .

Завдання. Чи належить точка рівняння кола

Рішення.
Якщо точка належить колу, її координати задовольняють рівнянню окружности.
Щоб перевірити, чи належить кола точка із заданими координатами, підставимо координати точки в рівняння заданого кола.

В рівняння ( x - 2) 2 + (y + 3) 2 = 16
підставимо, за умовою, координати точки А(2;3), тобто
x = 2
y = 3

Перевіримо істинність здобутої рівності
(x - 2) 2 + (y + 3) 2 = 16
(2 - 2) 2 + (3 + 3) 2 = 16
0 + 36 = 16 рівність невірна

Таким чином, задана точка не належитьзаданому рівнянню кола.

Нехай коло має радіус , а її центр знаходиться в точці
. Крапка
лежить на колі тоді і лише тоді, коли модуль вектора
дорівнює , тобто. Остання рівність виконана тоді і лише тоді, коли

Рівняння (1) і є шуканим рівнянням кола.

Рівняння прямої, що проходить через цю точку, перпендикулярно даному вектору

перпендикулярно вектору
.

Крапка

і
перпендикулярні. Вектори
і
перпендикулярні тоді й тільки тоді, коли їхній скалярний твір дорівнює нулю, тобто
. Використовуючи формулу обчислення скалярного твору векторів, заданих своїми координатами, рівняння прямої прямої записуємо у вигляді

Розглянемо приклад.Знайти рівняння прямої, що проходить через

середину відрізка АВ перпендикулярно цьому відрізку якщо координати точок відповідно дорівнюють А(1;6), В(5;4).

Будемо міркувати так. Щоб знайти рівняння прямої, ми повинні знати точку, через яку ця пряма проходить, і вектор перпендикулярний до цієї прямої. Вектором, перпендикулярним даній прямий, буде вектор , оскільки, за умовою завдання, перпендикулярна пряма відрізку АВ. Крапку
визначимо із умови, що пряма проходить через середину АВ. Маємо. Таким чином
і рівняння набуде вигляду.

З'ясуємо питання, чи проходить ця пряма через точку М(7;3).

Маємо, отже, ця пряма не проходить через вказану точку.

Рівняння прямої, що проходить через дану точку, паралельно даному вектору

Нехай пряма проходить через точку
паралельно вектору
.

Крапка
лежить на прямій тоді і лише тоді, коли вектори
і
колінеарні. Вектори
і
колінеарні тоді і тільки тоді, коли їхні координати пропорційні, тобто

(3)

Отримане рівняння є рівнянням шуканої прямої.

Рівняння (3) подаємо у вигляді

, де приймає будь-які значення
.

Отже, можемо записати

, де
(4)

Система рівнянь (4) називається параметричними рівняннями прямої.

Розглянемо приклад.Знайти рівняння прямої, що проходить через точки . Ми можемо побудувати рівняння прямої, якщо знаємо точку та паралельний чи перпендикулярний їй вектор. Точка в наявності цілих дві. Але якщо дві точки лежать на прямій, то вектор, що їх з'єднує, буде паралельний цій прямій. Тому скористаємося рівнянням (3), взявши як вектор
вектор
. Отримуємо

(5)

Рівняння (5) називається рівнянням прямої, що проходить через дві дані точки.

Загальне рівняння прямої

Визначення.Загальним рівнянням лінії першого порядку на площині називається рівняння виду
, де
.

Теорема.Будь-яка пряма на площині може бути задана як рівняння лінії першого порядку, і будь-яке рівняння лінії першого порядку є рівнянням деякої прямої на площині.

Перша частина цієї теореми доводиться просто. На будь-якій прямій можна вказати деяку точку
перпендикулярний вектор
. Тоді, згідно (2), рівняння такої прямої має вигляд. Позначимо
. Тоді рівняння набуде вигляду
.

Тепер перейдемо до другої частини теореми. Нехай є рівняння
, де
. Вважатимемо для визначеності
.

Перепишемо рівняння у вигляді:

;

Розглянемо на площині крапку
, де
. Тоді отримане рівняння має вигляд і є рівнянням прямої, що проходить через точку
перпендикулярно вектору
. Теорему доведено.

У процесі доказу теореми ми принагідно довели

Твердження.Якщо є рівняння прямого виду
, то вектор
перпендикулярний даній прямий.

Рівняння виду
називається загальним рівняннямпрямий на площині.

Нехай є пряма
і крапка
. Потрібно визначити відстань від зазначеної точки до прямої.

Розглянемо довільну точку
на прямий. Маємо
. Відстань від крапки
до прямої і модулю проекції вектора
на вектор
, перпендикулярний даній прямій. Маємо

,

перетворюючи, отримуємо формулу:

Нехай дані дві прямі, задані загальними рівняннями

,
. Тоді вектори

перпендикулярні першій та другій прямій відповідно. Кут
між прямими дорівнює куту між векторами
,
.

Тоді формула для визначення кута між прямими має вигляд:

.

Умова перпендикулярності прямих має вигляд:

.

Прямі паралельні або збігаються тоді і лише тоді, коли вектори

колінеарні. При цьому умова збігу прямих має вигляд:
,

а умова відсутності перетину записується у вигляді:
. Останні дві умови доведіть самостійно.

Досліджуємо характер поведінки прямої за її загальним рівнянням.

Нехай дано загальне рівняння прямої
. Якщо
, То пряма проходить через початок координат.

Розглянемо випадок, коли жоден з коефіцієнтів не дорівнює нулю
. Рівняння перепишемо у вигляді:

,

,

Де
. З'ясуємо зміст параметрів
. Знайдемо точки перетину прямої з осями координат. При
маємо
, а при
маємо
. Тобто
- це відрізки, які відсікає пряма на координатних осях. Тому рівняння
називається рівнянням прямої у відрізках.

В разі
маємо

. В разі
маємо
. Тобто пряма буде паралельна до осі .

Нагадаємо, що кутовим коефіцієнтом прямої називається тангенс кута нахилу цієї прямої до осі
. Нехай пряма відсікає на осі відрізок і має кутовий коефіцієнт . Нехай крапка
лежить на цій

Тоді
==. І рівняння прямої запишеться у вигляді

.

Нехай пряма проходить через точку
і має кутовий коефіцієнт . Нехай крапка
лежить на цій прямій.

Тоді =
.

Отримане рівняння називається рівнянням прямої, що проходить через дану точку із заданим кутовим коефіцієнтом.

Нехай дані дві прямі
,
. Позначимо
- Кут між ними. Нехай ,кути нахилу до осі Х відповідних прямих

Тоді
=
,
.

Тоді умова паралельності прямих має вигляд
, а умова перпендикулярності

На закінчення розглянемо дві задачі.

Завдання . Вершини трикутника АВС мають координати: A(4;2), B(10;10), C(20;14).

Знайти: а) рівняння та довжину медіани, проведеної з вершини А;

б) рівняння та довжину висоти, проведеної з вершини А;

в) рівняння бісектриси, проведеної з вершини А;

Визначимо рівняння медіани АМ.

Точка М() середина відрізка НД.

Тоді , . Отже, точка М має координати M(15; 17). Рівняння медіани мовою аналітичної геометрії це рівняння прямої, що проходить через точку А(4;2) паралельно вектору =(11;15). Тоді рівняння медіани має вигляд. Довжина медіани АМ= .

Рівняння висоти AS - це рівняння прямої, що проходить через точку А(4;2) перпендикулярно до вектора =(10;4). Тоді рівняння висоти має вигляд 10(x-4)+4(y-2)=0, 5x+2y-24=0.

Довжина висоти - це відстань від точки А (4; 2) до прямої ПС. Ця пряма проходить через точку B(10;10) паралельно вектору =(10;4). Її рівняння має вигляд 2x-5y+30=0. Відстань AS від точки А(4;2) до прямої ВС, отже, дорівнює AS= .

Для визначення рівняння бісектриси знайдемо вектор паралельний цій прямій. Для цього скористаємось властивістю діагоналі ромба. Якщо від точки А відкласти одиничні вектори однаково спрямовані з векторами, то вектор, що дорівнює їх сумі, буде паралельний бісектрисі. Тоді маємо = +.

={6;8}, , ={16,12}, .

Тоді = Як напрямний вектор шуканої прямої може служити вектор=(1;1), колінеарний даному. Тоді рівняння шуканої прямої має бачили x-y-2 = 0.

Завдання.Річка протікає по прямій лінії, що проходить через точки А(4; 3) і В (20; 11). У точці С(4;8) живе Червона Шапочка, а точці D(13;20) її бабуся. Щоранку Червона Шапочка бере порожнє відро з дому, йде на річку, черпає воду та відносить її бабусі. Знайти найкоротший шлях для Червоної Шапочки.

Знайдемо точку Е, симетричну бабусі щодо річки.

Для цього спочатку знайдемо рівняння прямої, якою тече річка. Це рівняння можна розглядати як рівняння прямої, що проходить через точку А(4;3) паралельно вектору . Тоді рівняння прямої АВ має вигляд.

Далі знайдемо рівняння прямої DE, що проходить через точку D перпендикулярно АВ. Його можна розглядати, як рівняння прямої, що проходить через точку D, перпендикулярно вектору
. Маємо

Тепер знайдемо точку S – проекцію точки D на пряму АВ, як перетин прямих АВ та DE. Маємо систему рівнянь

.

Отже, точка має координати S(18;10).

Оскільки S середина відрізка DE, то .

Аналогічно.

Отже, точка Е має координати Е(23; 0).

Знайдемо рівняння прямої РЄ, знаючи координати двох точок цієї прямої

Точку М знайдемо як перетин прямих АВ та РЄ.

Маємо систему рівнянь

.

Отже, точка М має координати
.

Тема 2.Концепція рівняння поверхні в просторі. Рівняння сфери. Рівняння площини, що проходить через цю точку перпендикулярно даному вектору. Загальне рівняння площини та її дослідження Умова паралельності двох площин. Відстань від точки до площини. Концепція рівняння лінії. Пряма лінія у просторі. Канонічні та параметричні рівняння прямої у просторі. Рівняння прямої, що проходить через дві дані точки. Умови паралельності та перпендикулярності прямої та площини.

Спочатку дамо визначення поняття рівняння поверхні в просторі.

Нехай у просторі
задана деяка поверхня . Рівняння
називається рівнянням поверхні , якщо виконано дві умови:

1.для будь-якої точки
з координатами
, що лежить на поверхні, виконано
, тобто її координати задовольняють рівняння поверхні;

2. будь-яка точка
координати якої задовольняють рівняння
лежить на лінії.

Визначення 1 . Числовою віссю ( числової прямої, координатної прямої) Ox називають пряму лінію, на якій точка O обрана початком відліку (початком координат)(рис.1), напрямок

O → x

вказано як позитивного спрямуванняі відзначено відрізок, довжина якого прийнята за одиницю довжини.

Визначення 2 . Відрізок, довжина якого прийнята за одиницю довжини називають масштабом .

Кожна точка числової осі має координату , що є речовим числом. Координата точки O дорівнює нулю. Координата довільної точки A, що лежить на промені Ox, дорівнює довжині відрізка OA. Координата довільної точки A числової осі, що не лежить на промені Ox негативна, а по абсолютній величині дорівнює довжині відрізка OA .

Визначення 3 . Прямокутною декартовою системою координат Oxy на площиніназивають дві взаємно перпендикулярнихчислових осі Ox і Oy з однаковими масштабамиі загальним початком відлікуу точці O , причому таких, що поворот від променя Ox на кут 90 ° до променя Oy здійснюється у напрямку проти ходу годинникової стрілки(Рис.2).

Зауваження. Прямокутну декартову систему координат Oxy , зображену малюнку 2, називають правою системою координат, на відміну від лівих систем координат, В яких поворот променя Ox на кут 90° до променя Oy здійснюється в напрямку годинникової стрілки. У цьому довіднику ми розглядаємо лише праві системи координат, не обговорюючи цього особливо.

Якщо на площині ввести якусь систему прямокутних декартових координат Oxy, то кожна точка площини придбає дві координати – абсцисуі ординату, що обчислюються таким чином. Нехай A – довільна точка площини. Опустимо з точки A перпендикуляри AA 1 та AA 2 на прямі Ox та Oy відповідно (рис.3).

Визначення 4 . Абсцисою точки A називають координату точки A 1 на числовій осі Ox ординатою точки A називають координату точки A 2 на числовій осі Oy.

Позначення. Координати (абсцису та ординату) точки A у прямокутній декартовій системі координат Oxy (рис.4) прийнято позначати A(x;y) або A = (x; y).

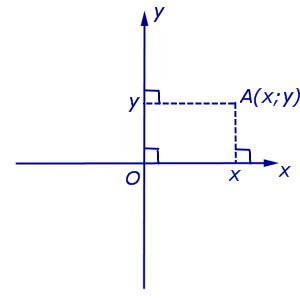
Зауваження. Точка O, звана початком координат, має координати O(0 ; 0) .

Визначення 5 . У прямокутній декартовій системі координат Oxy числову вісь Ox називають віссю абсцис, а числову вісь Oy називають віссю ординат (рис. 5).

Визначення 6 . Кожна прямокутна декартова система координат ділить площину на 4 чверті (квадранту), нумерація яких показана малюнку 5.

Визначення 7 . Площина, на якій задана прямокутна декартова система координат, називають координатною площиною.

Зауваження. Вісь абсцис задається на координатній площині рівнянням y= 0 , вісь ординат задається на координатній площині рівнянням x = 0.

Твердження 1 . Відстань між двома точкамикоординатної площини

A 1 (x 1 ;y 1) і A 2 (x 2 ;y 2)

обчислюється за формулою

Доведення . Розглянемо рисунок 6.

Коломназивається безліч точок площини, рівновіддалених від цієї точки, яка називається центром.

Якщо точка С – центр кола, R – її радіус, а М – довільна точка кола, то за визначенням кола

Рівність (1) є рівняння коларадіуса R з центром у точці С.

Нехай на площині задано прямокутну декартову систему координат (рис. 104) і точку С( а; b) - Центр кола радіуса R. Нехай М( х; у) - довільна точка цього кола.

Оскільки |СМ| = \(\sqrt((x - a)^2 + (у - b)^2) \), то рівняння (1) можна записати так:

\(\sqrt((x - a)^2 + (у - b)^2) \) = R

(x - a) 2 + (у - b) 2 = R 2 (2)

Рівняння (2) називають загальним рівнянням колаабо рівнянням кола радіуса R з центром у точці ( а; b). Наприклад, рівняння

(x - l) 2 + ( y + 3) 2 = 25

є рівняння кола радіуса R = 5 із центром у точці (1; -3).

Якщо центр кола збігається з початком координат, то рівняння (2) набуває вигляду

x 2 + у 2 = R2. (3)

Рівняння (3) називають канонічним рівнянням кола .

Завдання 1.Написати рівняння кола радіуса R = 7 із центром на початку координат.

Безпосереднім підстановленням значення радіуса в рівняння (3) отримаємо

x 2 + у 2 = 49.

Завдання 2.Написати рівняння кола радіуса R = 9 із центром у точці С(3; -6).

Підставивши значення координат точки С та значення радіуса у формулу (2), отримаємо

(х - 3) 2 + (у- (-6)) 2 = 81 або ( х - 3) 2 + (у + 6) 2 = 81.

Завдання 3.Знайти центр і радіус кола

(х + 3) 2 + (у-5) 2 =100.

Порівнюючи дане рівняння із загальним рівнянням кола (2), бачимо, що а = -3, b= 5, R = 10. Отже, С(-3; 5), R = 10.

Завдання 4.Довести, що рівняння

x 2 + у 2 + 4х - 2y - 4 = 0

є рівнянням кола. Знайти її центр та радіус.

Перетворимо ліву частину цього рівняння:

x 2 + 4х + 4- 4 + у 2 - 2у +1-1-4 = 0

(х + 2) 2 + (у - 1) 2 = 9.

Це рівняння є рівнянням кола з центром у точці (-2; 1); радіус кола дорівнює 3.

Завдання 5.Написати рівняння кола з центром у точці С(-1; -1), що стосується прямої АВ, якщо A (2; -1), B(- 1; 3).

Напишемо рівняння прямої АВ:

або 4 х + 3y-5 = 0.

Оскільки коло стосується цієї прямої, то радіус, проведений в точку торкання, перпендикулярний до цієї прямої. Для відшукання радіусу необхідно знайти відстань від точки С(-1; -1) - центру кола до прямої 4 х + 3y-5 = 0:

Напишемо рівняння шуканого кола

(x +1) 2 + (y +1) 2 = 144 / 25

Нехай у прямокутній системі координат дане коло x 2 + у 2 = R2. Розглянемо її довільну точку М( х; у) (рис. 105).

Нехай радіус-вектор OM> точки М утворює кут величини tз позитивним напрямом осі х, тоді абсцису та ординату точки М змінюються в залежності від t

(0 tх і у через t, знаходимо

x= R cos t ; y= R sin t , 0 t

Рівняння (4) називаються параметричними рівняннями кола з центром на початку координат.

Завдання 6.Окружність задана рівняннями

x= \(\sqrt(3)\)cos t, y= \(\sqrt(3)\)sin t, 0 t

Записати канонічне рівняння цього кола.

З умови випливає x 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складаючи ці рівності почленно, отримуємо

x 2 + у 2 = 3 (cos 2 t+ sin 2 t)

або x 2 + у 2 = 3

Побудувати функцію

Ми пропонуємо до вашої уваги сервіс з потроєння графіків функцій онлайн, всі права на який належать компанії Desmos. Для введення функцій скористайтесь лівою колонкою. Можна вводити вручну або за допомогою віртуальної клавіатури внизу вікна. Для збільшення вікна з графіком можна приховати як ліву колонку, і віртуальну клавіатуру.

Переваги побудови графіків онлайн

• Візуальне відображення функцій, що вводяться
• Побудова дуже складних графіків
• Побудова графіків, заданих неявно (наприклад, еліпс x^2/9+y^2/16=1)
• Можливість зберігати графіки та отримувати на них посилання, яке стає доступним для всіх в інтернеті.
• Управління масштабом, кольором ліній
• Можливість побудови графіків за точками, використання констант
• Побудова одночасно кількох графіків функцій
• Побудова графіків у полярній системі координат (використовуйте r та θ(\theta))

З нами легко в режимі онлайн будувати графіки різної складності. Побудова провадиться миттєво. Сервіс затребуваний знаходження точок перетину функцій, зображення графіків для подальшого їх переміщення у Word документ як ілюстрацій під час вирішення завдань, для аналізу поведінкових особливостей графіків функций. Оптимальним браузером для роботи з графіками на цій сторінці є Google Chrome. У разі використання інших браузерів коректність роботи не гарантується.