Дайте поняття проблеми
Проблема - складне теоретичне чи практичне питання, що потребує вивчення, вирішення; у науці - суперечлива ситуація, що у вигляді протилежних позицій у поясненні будь-яких явищ, об'єктів, процесів і потребує адекватної теорії її вирішення. Важливою передумовою успішного вирішення пробору. проблеми служить її правильна постановка.
Що розуміється під умовами вибору?
Перш ніж розглядати можливі варіантивирішення проблеми, керівнику необхідно визначити показники, якими буде проводитися порівняння альтернатив і вибір найкращої. Ці показники прийнято називати критерієм вибору.
Яке рішення вважатимуться оптимальним?
В ідеалі можна виявити всі можливі альтернативні шляхи вирішення проблеми, тільки в цьому випадку рішення може бути оптимальним. Однак на практиці керівник не має таких запасів знань і часу, щоб сформулювати та оцінити кожну можливу альтернативу. Тому вони шукають не оптимальний, а досить добрий, прийнятний варіант, що дозволяє зняти проблему, і допомагають відсікти заздалегідь непридатні альтернативи критерію вибору, визначені на попередньому етапі.
Завдання лінійного програмування (ЗЛП) це завдання знаходження найбільшого (або найменшого) значення лінійної функціїна опуклій багатогранній множині.
Симплекс метод – це метод розв'язання задачі лінійного програмування. Суть методу полягає у знаходженні початкового допустимого плану, і в подальшому поліпшенні плану до досягнення максимального (або мінімального) значення цільової функції в даній багатогранній опуклій множині або з'ясування нерозв'язності задачі.
Розглянемо наступне завдання лінійного програмування у канонічній формі:
| (1) |
| (2) |
| (3) |
Метод штучного базису
Як було зазначено вище, для задачі, записаної в канонічній формі, якщо серед векторів стовпців матриці Aє mодиничних і лінійно незалежних можна безпосередньо вказати опорний план. Однак для багатьох завдань лінійного програмування, записаних у канонічній формі та мають опорні плани, серед векторів стовпців матриці Aне завжди є mпоодиноких та лінійно незалежних. Розглянемо таке завдання:
Нехай потрібно знайти максимум функції
за умов
де перші nелементи нулі. Змінні ![]() називаються штучними. Вектори стовпці
називаються штучними. Вектори стовпці
  | (28) |
утворюють так званий штучний базис m-вимірного векторного простору.
Оскільки розширена задача має опорний план, її рішення можна знайти симплекс методом.
Теорема 4. Якщо оптимальному плані ![]() розширеного завдання (24)-(26) значення штучних змінних
розширеного завдання (24)-(26) значення штучних змінних ![]() , то
, то ![]() є оптимальним планом завдання (21)-(23).
є оптимальним планом завдання (21)-(23).
Таким чином, якщо в знайденому оптимальному плані розширеної задачі, значення штучних змінних дорівнюють нулю, то отримано оптимальний план вихідної задачі. Зупинимося докладніше на знаходженні рішення розширеного завдання.
Значення цільової функції при опорному плані (27):
Помічаємо, що F(X)і складаються з двох незалежних частин, одна з яких залежить від M, а інша – ні.
Після обчислення F(X)та їх значення, а також вихідні дані розширеної задачі заносять у симплекс таблицю, як було показано вище. Різниця полягає лише в тому, що дана таблиця містить один рядок більше, ніж звичайна симплекс таблиця. При цьому ( m+1)-ю рядок поміщають коефіцієнти, що не містять M, а в ( m+2)-й рядок − коефіцієнти при M.
При переході від одного опорного плану до іншого, базис вводять вектор, відповідний найбільшому по абсолютної величининегативному числу ( m+2) рядки. Штучний вектор, виключений з базису немає сенсу знову ввести базис. При переході до іншого опорного плану може статися так, що жоден із штучних векторів з базису не буде виключений. Перерахунок симплекс таблиці при переході від одного опорного плану до іншого виробляють за звичайними правилами симплекс методу (див. вище).
Ітераційний процес ведуть по m+2 рядку до тих пір, поки елементи m+2 рядки, що відповідають змінним ![]() не стануть невід'ємними. При цьому якщо штучні змінні виключені з базису, то знайдений план розширеної задачі відповідає деякому опорному плану вихідної задачі.
не стануть невід'ємними. При цьому якщо штучні змінні виключені з базису, то знайдений план розширеної задачі відповідає деякому опорному плану вихідної задачі.
m+2 рядки, стовпця x 0 негативний, то вихідне завдання немає рішення.
Якщо ж не всі штучні змінні виключені з базису та елемент m+2 рядки, стовпця x 0 дорівнює нулю, то опорний план вихідного завдання є виродженим і базис містить щонайменше один із векторів штучного базису.
Якщо вихідне завдання містить кілька одиничних векторів, їх слід включити в штучний базис.
Якщо під час ітерацій m+2 рядок більше не містить негативних елементів, то ітераційний процес продовжують з m+1 рядком, доки знайдено оптимальний план розширеної завдання чи виявлено нерозв'язність задачи.
Таким чином, процес знаходження рішення задачі лінійного програмування (21)-(23) методом штучного базису включає такі основні етапи:
- Складають розширене завдання (24) - (26).
- Знаходять опорний план розширеного завдання.
- Використовуючи симплекс метод виключають штучні вектори з базису. В результаті знаходять опорний план вихідного завдання або фіксують нерозв'язність.
- Використовуючи знайдений опорний план ЗЛП (21)-(23), або знаходять оптимальний план вихідної задачі, або встановлюють її нерозв'язність.
Для вирішення задач лінійного програмування онлайн, використовуйте калькулятор
Загальне завдання лінійного програмування (ОЗЛП) формулюється так – знайти змінні завдання x 1 , x 2 , ..., x n, які забезпечують екстремум цільової функції
Допустимим рішенням (планом) задачі лінійного програмування (ЗЛП) називається будь-який n-мірний вектор X=(x 1 , x 2 , ..., x n), що задовольняє системі обмежень рівностей та нерівностей. Безліч допустимих розв'язків задачі утворює область допустимих розв'язків D.
Оптимальним рішенням (планом) задачі лінійного програмування називається таке допустиме рішення, при якому цільова функція Z(X) досягає екстремуму.
Канонічна задача лінійного програмування (КЗЛП) має вигляд
 (1.2)
(1.2)
Вона відрізняється від ОЗЛП тим, що її система обмежень є лише системою рівнянь і всі змінні неотрицательные.
Приведення ОЗЛП до канонічного виду ЗЛП:
Щоб замінити вихідне завдання мінімізації на задачу максимізації (або навпаки задачу максимізації задачу мінімізації) досить цільову функцію помножити на «-1» і шукати максимум (мінімум) отриманої функції;
Якщо серед обмежень є нерівності, то шляхом запровадження додаткових невід'ємних змінних x n +1 ≥ 0 вони перетворюються на рівності:
нерівність a i 1 x 1 +…+a in x n ≥ b i замінюється на рівність a i 1 x 1 +…+a in x n+ x n +1 = b i ,
нерівність a i 1 x 1 +…+a in x n ≤ b i замінюється на рівність a i 1 x 1 +…+a in x n+ x n +1 = b i;
Якщо деяка змінна x k не має обмежень по знаку, то вона замінюється (у цільовій функції і в усіх обмеженнях) різницею між двома новими невід'ємними змінними: x k = x" k – x” k , де x" k ≥ 0. x” k ≥ 0.
Графічний метод вирішення ЗЛП із двома невідомими
ЗЛП із двома невідомими має вигляд:

Метод ґрунтується на можливості графічного зображення області допустимих рішень та знаходженні серед них оптимального рішення.
Область допустимих розв'язків (ОДР) задачі є опуклим багатокутником і будується як перетин (загальна частина) областей розв'язків кожної з нерівностей обмежень задачі.
Областю розв'язання нерівності a i 1 x 1 +a i 2 x 2 ≤ b i є одна з двох напівплощин, на які пряма a i 1 x 1 +a i 2 x 2 = b i , що відповідає цій нерівності, ділить координатну площину. Щоб визначити, яка з двох напівплощин є областю рішень, достатньо координати будь-якої точки, що не лежить на прямій, що розділяє підставити в нерівність:
Якщо нерівність справедлива, то областю рішень є напівплощина, що містить цю точку;
Якщо нерівність не справедлива, то областю рішень є напівплощина, що не містить цієї точки.
Для знаходження серед допустимих рішень оптимального використовуються лінії рівня.
Лінією рівня називається пряма з 1 x 1 +з 2 x 2 = l, де l= const, де цільова функція завдання приймає постійне значення. Усі лінії рівня паралельні між собою.
Градієнт цільової функції grad Z(X) задає вектор нормалі C = (c 1 , c 2) ліній рівня. Цільова функція на лініях рівня зростає, якщо лінії рівня переміщати у напрямку їх нормалі, і меншає – у протилежному напрямку.
Опорною прямою називається лінія рівня, яка має хоча б одну загальну точку з ОДР і по відношенню до якої ОДР знаходиться в одній із напівплощин. ОДР завдання має не більше двох опорних прямих.
Оптимальне рішення ЗЛП лежить на опорній прямій у кутовій точці багатокутника ОДР. ЗЛП має єдине рішення, якщо опорна пряма проходить через одну кутову точку ОДР, безліч рішень, якщо опорна пряма проходить через ребро багатокутника ОДР. ЗЛП немає рішення, якщо ОДР є порожнім безліччю (коли система обмежень несовместна) і якщо ОДР необмежена у бік екстремуму (цільова функція необмежена).
Алгоритм графічного методу вирішення ЗЛП із двома невідомими:
Побудувати ОДР.
Побудувати вектор нормалі C = (c 1 , c 2) та лінію рівня з 1 x 1 +з 2 x 2 = 0, що проходить через початок координат та перпендикулярну вектору З.
Пересувати лінію рівня до опорної прямої у напрямку вектора Зу завданні на max, або у протилежному напрямку – у завданні на min.
Якщо при переміщенні лінії рівня в напрямку екстремуму ОДР йде в нескінченність, то ЗЛП не має рішення через необмеженість цільової функції.
Якщо ЗЛП має оптимальне рішення, то для його знаходження вирішити спільно рівняння прямих, що обмежують ОДР та мають спільні точки з опорною прямою. Якщо екстремум досягається у двох кутових точках, то ЗЛП має безліч рішень, що належать ребру ОДР, обмеженому цими кутовими точками. У разі обчислюються координати обох кутових точок.
Обчислити значення цільової функції у точці екстремуму.
Симплекс-метод рішення ЗЛП
Симплекс-метод ґрунтується на таких положеннях:
ОДР задачі лінійного програмування є опуклим множиною з кінцевим числом кутових точок;
Оптимальним рішенням ЗЛП є з кутових точок ОДР. Кутові точки ОДР алгебраїчно представляють деякі базисні (опорні) рішення системи обмежень ЗЛП.
Базовим (опорним) рішенням ЗЛП називається таке допустиме рішення X 0 =(x 10 , x 20 , ..., x m 0 , 0, ... 0), для якого вектори умов (стовпці коефіцієнтів за невідомих у системі обмежень) лінійно незалежні.
Ненульові координати x 10 , x 20 , ..., x m 0 рішення X 0 називаються базисними змінними, координати рішення, що залишилися X 0 – вільними змінними. Число відмінних від нуля координат опорного рішення не може бути більшим за ранг rсистеми обмежень ЗЛП (числа лінійно незалежних рівнянь у системі обмежень ЗЛП). p align="justify"> Далі вважаємо, що система обмежень ЗЛП складається з лінійно незалежних рівнянь, тобто. r = m.
Сенс симплекс-метода полягає у цілеспрямованому переході від одного опорного рішення ЗЛП до іншого (тобто від однієї кутової точки ОДР до іншої) у напрямку екстремуму і полягає в послідовності етапів:
Знайти початкове опорне рішення;
здійснити перехід від одного опорного рішення до іншого;
Визначити критерій досягнення оптимального рішення чи зробити висновок про відсутність рішення.
Алгоритм виконанняСимплекс-метод ЗЛП
Алгоритм симплекс-метода здійснює перехід від одного опорного рішення ЗЛП до іншого у напрямку екстремуму цільової функції.
Нехай ЗЛП задана в канонічному вигляді (1.2) та виконано умову
b i ≥ 0, i=1,2,…,m, (1.3)
співвідношення (1.3) завжди можна виконати, домноживши відповідне рівняння на «-1» у разі негативності b i. Також вважаємо, що система рівнянь в обмеженнях задачі (1.2) лінійно незалежна та має ранг r = m. У цьому вектор опорного рішення має mненульових координат.
Нехай вихідне завдання (1.2), (1.3) наведено до виду, де базисні змінні x 1 , x 2 , ..., x m виражені через вільні змінні x m + 1 , x m + 2 , ..., x n
 (1.4)
(1.4)
На основі цих співвідношень збудуємо таблицю 1
Таблиця 1.

Таблиця 1 називається симплекс-таблицею. Усі подальші перетворення пов'язані із змінами змісту цієї таблиці.
Алгоритм зімплекс-методу:
1. В останньому рядку Zсимплекс-таблиці у задачі на min знаходять найменший позитивний елемент (у задачі на max - найменший негативний елемент), крім вільного члена. Стовпець, що відповідає цьому елементу, називається роздільною здатністю.
2. Обчислюють відношення вільних членів до позитивних елементів роздільного стовпця (симплекс-відношення). Знаходять найменше з цих симплекс - відносин, воно відповідає роздільній здатності.
3. На перетині роздільної здатності і роздільного стовпця знаходиться роздільна здатність.
4. Якщо є кілька однакових за величиною симплекс - відносин, то вибирають будь-яке з них. Те саме стосується позитивних елементів останнього рядка симлекс - таблиці.
5. Після знаходження роздільного елемента переходять до наступної таблиці. Невідомі змінні, що відповідають роздільній здатності і стовпцю, змінюють місцями. При цьому базова змінна стає вільною змінною і навпаки. Симплекс - таблиця перетворюється в такий спосіб (таблиця 2):
Таблиця 2

6. Елемент таблиці 2, відповідний роздільному елементу таблиці 1, дорівнює зворотній величині роздільної здатності елемента.
7. Елементи рядка таблиці 2, відповідні елементам роздільної здатності таблиці 1, виходять шляхом поділу відповідних елементів таблиці 1 на роздільний елемент.
8. Елементи стовпця таблиці 2, відповідні елементам роздільної здатності стовпця таблиці 1, виходять шляхом поділу відповідних елементів таблиці 1 на роздільний елемент і беруться з протилежним знаком.
9. Інші елементи обчислюються за правилу прямокутника: подумки викреслюємо прямокутник у таблиці 1, одна вершина якого збігається з роздільною здатністю елементом (Ре), а інша – з елементом, який ми шукаємо; позначимо елемент у новій таблиці 2 через (Не), а елемент, що стоїть цьому ж місці у старій таблиці 1 – через (Се). Інші дві вершини А і В доповнюють фігуру до прямокутника. Тоді шуканий елемент Не з таблиці 2 дорівнює Не = Се - А * В / Ре.
10. Критерій оптимальності. Як тільки вийде таблиця, у якої в останньому рядку в задачі на min всі елементи негативні (в задачі на max всі позитивні елементи), вважається, що екстремум знайдений. Оптимальне значення цільової функції дорівнює вільному члену рядку Z, а оптимальне рішення визначається вільними членами при базисних змінних. Усі вільні змінні вважаються рівними нулю.
11.Если у вирішальному стовпці всі елементи негативні, то завдання немає рішень (мінімум не досягається).
Метод штучного базису рішення ЗЛП
Алгоритм симплекс-метода застосовний, якщо виділено якесь опорне рішення ЗЛП, тобто, вихідна ЗЛП (1.2) наведена до виду (1.4). Метод штучного базису пропонує процедуру побудови такого опорного рішення.
Метод штучного базису заснований на введенні штучних базисних змінних y 1 , y 2 ,…, y m, за допомогою яких система обмежень ЗЛП (2.2)
 (1.5)
(1.5)
може бути перетворена на вигляд
 (1.6)
(1.6)
Системи (1.5) та (1.6) будуть еквівалентні в тому випадку, якщо всі y i дорівнюватимуть нулю. Як і раніше ми вважаємо, що всі b i ≥ 0. Для того щоб у i дорівнювали 0, ми повинні перетворити завдання таким чином, щоб усі штучні базові змінні y i перейшли у вільні змінні. Такий перехід можна зробити алгоритмом симплекс методу щодо додаткової цільової функції
F(y) = y 1 + y 2 + ... + y m = d 0 – (d 1 x 1 +d 2 x 2 +…+d n x n). (2.7)
Вихідна симплекс таблиця для даного методу має вигляд

Спочатку симплекс таблиця перетворюється щодо цільової функції F(y) До отримання опорного рішення. Опорне рішення знайдено, коли виконано наступний критерій: F(y) = 0 і всі штучні змінні у i переведені у вільні змінні. Потім з симплекс таблиці викреслюється рядок для F(y) і стовпці для у i і вирішують завдання для вихідної цільової функції Z(x) До отримання оптимального рішення.
Теорема 4.1. Якщо задачі лінійного програмування на максимум (мінімум) хоча б одного вектора умов оцінка розкладання по базису невиродженого опорного рішення негативна (позитивна), то опорне рішення може бути поліпшено, т. е. можна знайти нове опорне рішення, у якому значення цільової функції буде більше (менше).
Доведення. Нехай вирішується завдання на максимум, яке має невироджене опорне рішення,  , та оцінка розкладання деякого вектора умов негативна (
, та оцінка розкладання деякого вектора умов негативна (  ).
).
Перейдемо до нового опорного рішення, введемо в базис вектор і виключимо з базису вектор. У цьому випадку збільшення цільової функції дорівнює
Рішення невироджене, тому параметр , що обчислюється за формулою (4.5), відрізняється від нуля (> 0). Оскільки > 0,  , то
, то
Отже, значення цільової функції на новому опорному рішенні буде більшим, ніж на першому .
Доказ для завдання щонайменше аналогічний.
Наслідок 1(Умова найбільшого наближення до оптимального рішення). Для найбільшої зміни цільової функції при поліпшенні опорного рішення необхідно вибрати вектор, що виводиться з базису (з номером l) та введеного в базис (з номером k), виробляти з умов:
– у завданні на максимум  ; (4.10)
; (4.10)
– у завданні на мінімум  . (4.11)
. (4.11)
У спрощеному варіанті вибір вектора, що вводиться в базис, можна проводити за умов:
– у завданні на максимум  ; (4.12)
; (4.12)
– у завданні на мінімум  . (4.13)
. (4.13)
Цей варіант початку новому опорному рішенню зазвичай використовується при розрахунках на ЕОМ.
Наслідок 2(Ознака оптимальності опорного рішення). Опорне рішення задачі лінійного програмування на максимум (мінімум) є оптимальним, якщо для будь-якого вектора умов оцінка розкладання базисом опорного рішення невід'ємна (непозитивна), тобто.
– у завданні на максимум  ; (4.14)
; (4.14)
– у завданні на мінімум  . (4.15)
. (4.15)
Справді, якщо Z(x) ![]() ,
,  ,
,  , то
, то
тобто – оптимальне рішення. Для завдання мінімум доказ аналогічно.
Наслідок 3(Ознака єдиності оптимального рішення). Оптимальне рішення задачі лінійного програмування є єдиним, якщо для будь-якого вектора умов, що не входить до базису, оцінка відмінна від нуля, тобто.
Тут передбачається, що в базис оптимального рішення входять перші mвекторів.
Слідство 4(Ознака існування нескінченної множини оптимальних рішень). Завдання лінійного програмування має безліч оптимальних рішень, якщо вона має оптимальне рішення, при якому хоча б один з векторів умов, що не входять в базис оптимального рішення, має оцінку рівну нулю, тобто.
$ k Î { m+1,m+2, ..., n}:  . (4.17)
. (4.17)
Наслідок 5(Ознака відсутності оптимального рішення через необмеженість цільової функції). Завдання лінійного програмування немає рішення через необмеженості цільової функції, якщо якогось із векторів умов з оцінкою , суперечить ознаки оптимальності, серед коефіцієнтів розкладання по базису опорного рішення немає позитивного, тобто.
Універсальний метод розв'язання задач ЛП називається симплекс-методом. Застосування цього і його найчастіше зустрічається модифікації - двухфазного симплекс-метода.
При графічному способі вирішення завдань ЛП ми практично з безлічі вершин, що належать межі безлічі рішень системи нерівностей, вибрали таку вершину, в якій значення цільової функції досягало максимуму (мінімуму). У разі змінних цей метод цілком наочний і дозволяє швидко знаходити рішення задачі.
Якщо задачі три і більше змінних, а реальних економічних завданнях саме така ситуація, важко уявити наочно область рішень системи обмежень. Такі завдання вирішуються за допомогою симплекс-метода чи методом послідовних поліпшень. Ідея методу проста і полягає у наступному.
За певним правилом знаходиться первісний опорний план (деяка вершина області обмежень). Перевіряється, чи є план оптимальним. Якщо так, то завдання вирішено. Якщо ні, то переходимо до іншого покращеного плану – до іншої вершини. значення цільової функції у цьому плані (у цій вершині) явно краще, ніж у попередньої. Алгоритм переходу здійснюється за допомогою деякого обчислювального кроку, який зручно записувати у вигляді таблиць симплекс-таблицями . Так як вершин кінцеве число, то за кінцеве число кроків ми приходимо до раціонального рішення.
Розглянемо симплексний метод конкретному прикладі завдання упорядкування плану.
Ще раз зауважимо, що симплекс-метод застосуємо для вирішення канонічних завдань ЛП, наведених до спеціального вигляду, тобто мають базис, позитивні праві частини та цільову функцію, виражену через небазисні змінні. Якщо завдання не приведено до спеціального вигляду, то потрібні додаткові кроки, про які ми поговоримо пізніше.
Розглянемо завдання план виробництва, попередньо побудувавши модель і привівши її до спеціального виду.
Завдання.
Для виготовлення виробів Аі Усклад може відпустити сировини трохи більше 80 одиниць. Причому виготовлення виробу Авитрачається дві одиниці, а вироби У- Одна одиниця сировини. Потрібно спланувати виробництво так, щоб був забезпечений найбільший прибуток, якщо виробів Апотрібно виготовити не більше 50 шт., а виробів У- Не більше 40 шт. Причому прибуток від реалізації одного виробу А- 5 руб., а від У- 3 руб.
Побудуємо математичну модель, позначивши за х 1 кількість виробів А в плані, х 2 - кількість виробів У. тоді система обмежень буде виглядати так:
x 1 ≤50
x 2 ≤40
2x 1 +x 2 ≤80
x 1 ≥0, x 2 ≥0
5x 1 +3x 2 →max
Наведемо завдання до канонічного вигляду, ввівши додаткові змінні:
x 1 +x 3 =50
x 2 +x 4 =40
2x1+x2+x5=80
x 1 ≥0, x 2 ≥0
5x 1 +3x 2 →max
-F = -5x1 - 3x2 → min.
Це завдання має спеціальний вид (з базисом, праві частини невід'ємні). Її можна вирішити симплекс-методом.
Iетап.Запис завдання до симплекс-таблиці. Між системою обмежень задачі (3.10) та симплекс-таблицею взаємно-однозначна відповідність. Рядків у таблиці стільки, скільки рівностей у системі обмежень, а стовпців - стільки, скільки вільних змінних. Базові змінні заповнюють перший стовпець, вільні - верхній рядок таблиці. Нижній рядок називається індексним, у ньому записуються коефіцієнти при змінних у цільовій функції. У правому нижньому куті спочатку записується 0, якщо функції немає вільного члена; якщо є, то записуємо його із протилежним знаком. На цьому місці (у правому нижньому кутку) буде значення цільової функції, яке при переході від однієї таблиці до іншої повинне збільшуватися по модулю. Отже, нашій системі обмежень відповідає таблиця 3.4 і можна переходити до II етапу рішення.
Таблиця 3.4
|
базисні |
вільні |
||
IIетап. Перевірка опорного плану оптимальність.
Ця таблиця 3.4 відповідає наступний опорний план:
(х 1 , х 2 , х 3 , х 4 , х 5) = (0, 0, 50, 40, 80).
Вільні змінні х 1 , х 2 дорівнюють 0; х 1 = 0, х 2 = 0. А базисні змінні х 3 , х 4 , х 5 приймають значення х 3 = 50, х 4 = 40, х 5 = 80 – зі стовпця вільних членів. Значення цільової функції:
-F = - 5х 1 - 3х 2 = -5 · 0 - 3 · 0 = 0.
Наше завдання – перевірити, чи є даний опорний план оптимальним. для цього необхідно переглянути індексний рядок - рядок цільової функції F.
Можливі різні ситуації.
1. В індексній F-Рядок немає негативних елементів. Отже, план оптимальний, можна виписати розв'язання задачі. Цільова функція досягла свого оптимального значення, що дорівнює числу, що стоїть у правому нижньому кутку, взятому з протилежним знаком. Переходимо до IV етапу.
2. В індексному рядку є хоча б один негативний елемент, у стовпці якого немає позитивних. Тоді робимо висновок у тому, що цільова функція F→∞ необмежено зменшується.
3. В індексному рядку є негативний елемент, у стовпці якого є хоча б один позитивний. Тоді переходимо до наступного ІІІ етапу. перераховуємо таблицю, покращуючи опорний план.
IIIетап. Поліпшення опорного плану.
З негативних елементів індексної F-Рядки виберемо найбільший по модулю, назвемо відповідний йому стовпець роздільним і позначимо "".
Щоб вибрати роздільну здатність, необхідно обчислити відносини елементів стовпця вільних членів тількидо позитивнимелементам роздільного стовпця. Вибрати із отриманих відносин мінімальне. Відповідний елемент, на якому досягається мінімум, називається роздільною здатністю. Виділятимемо його квадратом.
У прикладі, елемент 2 - вирішальний. Рядок, що відповідає цьому елементу, теж називається роздільною (табл. 3.5).
Таблиця 3.5

Вибравши роздільну здатність, робимо перелік таблиці за правилами:
1. У новій таблиці таких самих розмірів, як і раніше, змінні роздільної здатності і стовпця змінюються місцями, що відповідає переходу до нового базису. У нашому прикладі: х 1 входить у базис, замість х 5 , яка виходить із базису і тепер вільна (табл. 3.6).
Таблиця 3.6
2. На місці роздільної здатності елемента 2 записуємо зворотне йому число ½.
3. Елементи роздільної здатності ділимо на роздільний елемент.
4. Елементи роздільної здатності ділимо на роздільний елемент і записуємо з протилежним знаком.
5. Щоб заповнити елементи таблиці 3.6, що залишилися, здійснюємо перерахунок за правилом прямокутника. Нехай ми хочемо порахувати елемент на місці 50.
З'єднуємо цей елемент подумки з вирішальним, знаходимо твір, віднімаємо твір елементів, що знаходяться на іншій діагоналі прямокутника, що вийшов. Різницю ділимо на роздільний елемент.

Отже, . Записуємо 10 на місце, де було 50. Аналогічно:
, ![]() , ,
, , ![]() .
.
Таблиця 3.7

Маємо нову таблицю 3.7, базисними змінними тепер є змінні (x 3 x 4 x 1). Значення цільової функції дорівнювало -200, тобто. поменшало. Щоб перевірити це базове рішення на оптимальність треба перейти знову до II етапу. Процес, очевидно, кінець, критерієм зупинки є пункт 1 і 2 II етапу.
Доведемо розв'язання задачі до кінця. Для цього перевіримо індексний рядок і, побачивши в ньому негативний елемент -½, назвемо відповідний йому стовпець роздільною здатністю і, згідно з III етапом, перерахуємо таблицю. Склавши відносини і вибравши серед них мінімальне = 40, визначили роздільну здатність елемент 1. Тепер перерахунок здійснюємо згідно з правилами 2-5.
Таблиця 3.8
Після перерахунку таблиці переконуємося, що у індексному рядку немає негативних елементів, отже, завдання вирішено, базисний план є оптимальним.
IVетап. Виписування раціонального рішення.
Якщо симплекс-метод зупинився згідно з пунктом 1 II етапу, рішення завдання виписується наступним чином. Базисні змінні набувають значення стовпця вільних членів відповідно. У нашому прикладі х 3 = 30, х 2 = 40, х 1 = 20. Вільні змінні дорівнюють 0, х 5 = 0, х 4 = 0. Цільова функція набуває значення останнього елемента стовпця вільних членів із протилежним знаком: - F = -220 → F= 220, у прикладі функція досліджувалася на min, і спочатку F→ max, тому фактично знак змінився двічі. Отже, х* = (20, 40, 30, 0, 0), F* = 220. Відповідь до завдання:
Необхідно до плану випуску включити 20 виробів типу А, 40 виробів типу В, при цьому прибуток буде максимальною і дорівнюватиме 220 руб.
Наприкінці цього параграфа наведемо блок-схему алгоритму симплекс-метода, яка в точності повторює етапи, але, можливо, для деяких читачів буде зручніша у користуванні, тому що стрілочки вказують чітку спрямованість дій.
Посилання над прямокутниками у блок-схемі показують, якого етапу чи підпункту належить відповідна група перетворень. правило знаходження початкового опорного плану буде сформульовано у пункті 3.7.

Приклад. Вирішити наступне завдання ЛП у канонічній формі симплекс-методом.
f(x)=x 1 +9x 2 +5x 3 +3x 4 +4x 5 +14x 6 → min
x 1 +x 4 =20
x 2 +x 5 =50
x 3 +x 6 =30
x 4 +x 5 +x 6 =60
x i ≥ 0, i = 1,…,6
Говорять, що завдання ЛП має канонічну форму, якщо всі обмеження (крім умов невід'ємності змінних) мають вигляд рівностей, а всі вільні члени невід'ємні. Отже, ми маємо завдання в канонічній формі.
Ідея симплекс-методу полягає у наступному. Спочатку потрібно визначити деяку (початкову) вершину багатогранника допустимих рішень (початкове допустиме базисне рішення). Потім слід перевірити це рішення на оптимальність. Якщо вона оптимальна, то рішення знайдено; якщо ні, то перейти до іншої вершини багатогранника і знову перевірити оптимальність. Зважаючи на кінцівку вершин багатогранника (наслідок кінцівки обмежень завдання ЛП) за кінцеве число "кроків" ми знайдемо шукану точку мінімуму або максимуму. Слід зазначити, що з переході від однієї вершини до іншої значення цільової функції зменшується (у задачі мінімум) чи зростає (у задачі максимум).
Таким чином, ідея симплекс-методу ґрунтується на трьох властивостях задачі ЛП.
Рішення.Щоб визначити початкове допустиме базисне рішення, тобто. щоб визначити базисні змінні, систему (5.6) потрібно призвести до "діагонального" вигляду. Застосовуючи метод Гауса (метод послідовного виключення невідомих), отримуємо з (5.6):
x 2 +x 1 +x 3 =40
x 4 +x 1 =20
x 5 -x 1 -x 3 = 10
x 6 +x 3 =30
Отже, базисними є змінні x 2 x 4 x 5 x 6їм надаємо значення, рівні вільним членам відповідних рядків: x 2 = 40, x 4 = 20, x 5 = 10, x 6 = 30,. Змінні x 1і x 3є небазисними: x 1 = 0, x 3 = 0.
Побудуємо початкове допустиме базисне рішення
x 0 = (0,40,0,20,10,30) (5.9)
Для перевірки оптимальності знайденого рішення x 0Необхідно з цільової функції виключити базові змінні (за допомогою системи (5.8)) і побудувати спеціальну симплекс таблицю.
Після виключення змінних цільову функцію зручно записати у вигляді:
f(x) = -7x 1 – 14x 3 +880 (5.10)
Тепер за допомогою (5.8) - (5.10) складаємо початкову симплекс-таблицю: 
У нульовий рядок записані коефіцієнти зі зворотним знаком відповідних змінних при цільовій функції. Критерій оптимальності (для завдання на пошук мінімуму): допустиме базисне рішення ( x 0) оптимально, якщо в нульовому рядку немає жодного строго позитивного числа (крім значення цільової функції (880)). Це поширюється і такі ітерації (таблиці). Елементи нульового рядка називатимемо оцінками стовпців.
Отже, початкове допустиме базисне рішення (5.9) неоптимально: 7>0, 14>0
.
У нульовому стовпчику записані значення базових змінних. Вони обов'язково мають бути невід'ємними (див. рівняння (5.7)). Від першого до четвертого рядка написані коефіцієнти змінних із системи (5.8).
Так як x 0неоптимально, треба перейти до іншої вершині багатогранника допустимих рішень (побудувати нове д.б.р.). Для цього потрібно знайти провідний елемент та провести певне перетворення (симплексне перетворення).
Спочатку знаходимо провідний елемент таблиці, який стоїть у перетині провідного стовпчика (стовпець з найбільшою позитивною оцінкою) та провідного рядка (рядки, що відповідає мінімальному співвідношенню елементів нульового стовпчика до відповідних елементів (строго позитивних) провідного стовпчика).
У таблиці 1 провідний стовпчик - третій стовпчик, і провідний рядок - четвертий рядок (min(40/1,30/1)=30/1)позначені стрілками, а провідний елемент – кружечком. Провідний елемент показує, що базову змінну x 6потрібно замінити на небазову x 3. Тоді новими базовими змінними будуть x 2 x 3 x 4 x 5, а небазисними - x 1 , x 6 ,. Це означає перехід до нової вершині багатогранника допустимих рішень. Щоб знайти значення координат нового допустимого базового рішення x 00потрібно будувати нову симплекс-таблицю і провести у ній елементарні перетворення:
а)всі елементи провідного рядка поділити на провідний елемент, перетворивши цим провідний елемент в 1 (для простоти викладок);
б)за допомогою провідного елемента (рівного 1) всі елементи провідного стовпчика перетворити на нулі (аналогічно методу виключення невідомих);
В результаті в нульовому стовпці отримано значення нових базисних змінних x 2 x 3 x 4 x 5(див. таблицю 2) – базисні компоненти нової вершини x 00(Небазисні компоненти x 1 = 0, x 6 = 0,).

Як показує таблиця 2, нове базисне рішення x 00 = (0,10,30,20,40,0)неоптимально (у нульовому рядку є невід'ємна оцінка 7). Тому із провідним елементом 1 (див. таблицю 2) будуємо нову симплекс-таблицу, тобто. будуємо нове допустиме базисне рішення 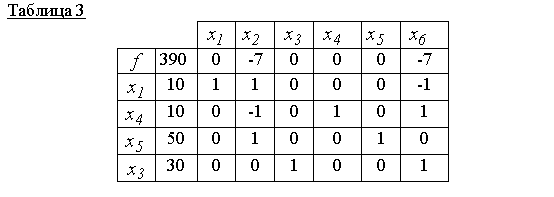
Таблиці 3 відповідає допустиме базисне рішення x 000 = (10,0,30,10,50,0)і його оптимально, т.к. в нульовому рядку немає позитивних оцінок. Тому f(x 000)=390є мінімальне значення цільової функції.
Відповідь: x 000 = (10, 0, 30, 10, 50, 0)- точка мінімуму, f(x 000)=390.
Умовно стандартне завдання лінійного програмування
Необхідно виконати у вказаному порядку такі завдання.- Знайти оптимальний план прямого завдання:
а) графічним методом;
б) симплекс-метод (для побудови вихідного опорного плану рекомендується використовувати метод штучного базису). - Побудувати подвійне завдання.
- Знайти оптимальний план двоїстої задачі з графічного рішення прямої, використовуючи умови, що доповнює нежорсткості.
- Знайти оптимальний план двоїстої задачі за першою теоремою двоїстості , використовуючи остаточну симплекс-таблицю, отриману під час вирішення прямої задачі (див. п. 1б). Перевірити твердження «значення цільових функцій пари двоїстих завдань на своїх оптимальних рішеннях збігаються».
- Подвійну задачу вирішити симплекс-методом, потім, використовуючи остаточну симплекс-таблицю двоїстої задачі знайти оптимальний план прямої задачі за першою теоремою двоїстості. Порівняти результат з результатом, отриманим графічним методом (див. п. 1а).
- Знайти оптимальне ціле рішення:
а) графічним методом;
б) Методом Гоморі.
Порівняти значення функцій цілочисленного та нецілочисленного рішень
Запитання для самоконтролю
- Як будується симплекс-таблиця?
- Як відображається зміна базису таблиці?
- Сформулюйте критерій зупинки симплекс-метода.
- Як організувати перерахунок таблиці?
- З якого рядка зручно розпочинати перерахунок таблиці?



